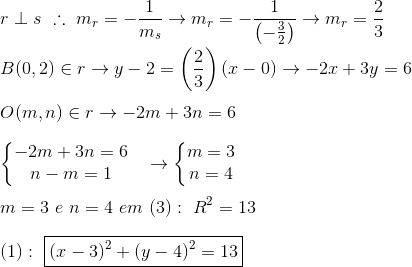Reta e Circunfereência
3 participantes
Página 1 de 1
Reta e Circunfereência
por Lolisa73 Sex 21 Jul 2017, 17:47
"Obtenha a circunferência que passa nos pontos A (1;1) e B (0;2) e tangência a reta (s) 3x + 2y -4 =0"
- (x-3)^2 + (y-4)^2 = 13:
Lolisa73- Padawan
- Mensagens : 85
Data de inscrição : 26/03/2016
Idade : 25
Localização : SP, SP, BR
Re: Reta e Circunfereência
por EsdrasCFOPM Sex 21 Jul 2017, 20:05
Sendo C(xc,yc) o centro, temos que dCA=dCB=dsC=r.
dCA=√[(xc-1)2+(yc-1)2]
dCB=√[(xc-0)2+(yc-2)2]
dsC=|3xc+2yc-4|/√(13)
(xc-1)2+(yc-1)2=(xc-0)2+(yc-2)2
xc2-2xc+1+yc2-2yc+1=xc2+yc2-4yc+4
2xc-2yc+2=0 --> xc-yc+1=0 --> xc=yc-1
√[(xc-0)2+(yc-2)2]=|3xc+2yc-4|/√(13)
√[(yc-1)2+(yc-2)2]=|3(yc-1)+2yc-4|/√(13)
{√[(yc-1)2+(yc-2)2]}2=[|5yc-7|/√(13)]2
(yc-1)2+(yc-2)2=(|5yc-7|)2/√(13)2
13(yc2-2yc+1+yc2-4yc+4)=25yc2-70yc+49
26yc2-78yc+65=25yc2-70yc+49
yc2-8yc+16=0
∆=64-4.1.16
∆=0
yc=8/2 --> yc=4 e xc=3
dCB=r=√[(xc-0)2+(yc-2)2]
r=√[(3)2+(4-2)2]
r=√13
(x-xc)2+(y-yc)2=r2
(x-3)2+(y-4)2=13
dCA=√[(xc-1)2+(yc-1)2]
dCB=√[(xc-0)2+(yc-2)2]
dsC=|3xc+2yc-4|/√(13)
(xc-1)2+(yc-1)2=(xc-0)2+(yc-2)2
xc2-2xc+1+yc2-2yc+1=xc2+yc2-4yc+4
2xc-2yc+2=0 --> xc-yc+1=0 --> xc=yc-1
√[(xc-0)2+(yc-2)2]=|3xc+2yc-4|/√(13)
√[(yc-1)2+(yc-2)2]=|3(yc-1)+2yc-4|/√(13)
{√[(yc-1)2+(yc-2)2]}2=[|5yc-7|/√(13)]2
(yc-1)2+(yc-2)2=(|5yc-7|)2/√(13)2
13(yc2-2yc+1+yc2-4yc+4)=25yc2-70yc+49
26yc2-78yc+65=25yc2-70yc+49
yc2-8yc+16=0
∆=64-4.1.16
∆=0
yc=8/2 --> yc=4 e xc=3
dCB=r=√[(xc-0)2+(yc-2)2]
r=√[(3)2+(4-2)2]
r=√13
(x-xc)2+(y-yc)2=r2
(x-3)2+(y-4)2=13
EsdrasCFOPM- Estrela Dourada
- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
Re: Reta e Circunfereência
por Giovana Martins Sex 21 Jul 2017, 21:04
Outro modo:
- Para B(0,2): 3.(0)+2.(2)-4=0 -> 0=0 ∴ B(0,2)∈s;
- Se B(0,2) pertence à reta e à circunferência, logo, B(0,2) é o ponto de tangência;
- Seja O(m,n) o centro da circunferência.
- Seja r a reta que contém o raio da circunferência. Esta reta é perpendicular à reta s e passa pelo ponto B(0,2). Logo:
____________________________________________
Charlotte de Witte - Universal Nation
Giovana Martins- Grande Mestre
- Mensagens : 8545
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Re: Reta e Circunfereência
por Lolisa73 Qua 26 Jul 2017, 13:07
Excelente!!! Muito obrigada, Esdras e Giovana!
Lolisa73- Padawan
- Mensagens : 85
Data de inscrição : 26/03/2016
Idade : 25
Localização : SP, SP, BR
Re: Reta e Circunfereência
por Giovana Martins Qua 26 Jul 2017, 13:53
De nada!
____________________________________________
Charlotte de Witte - Universal Nation
Giovana Martins- Grande Mestre
- Mensagens : 8545
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Tópicos semelhantes» Reta simétrica em relação à outra reta
» Equação da reta normal à reta tangente
» (Unesp) A reta r é perpendicular à reta -3x+4y-5=0 ...
» Reta simétrica à outra reta
» Parametrização da reta e reta tangente
» Equação da reta normal à reta tangente
» (Unesp) A reta r é perpendicular à reta -3x+4y-5=0 ...
» Reta simétrica à outra reta
» Parametrização da reta e reta tangente
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
