Triângulo Obtusângulo

Dado o triângulo obtusângulo ABC, obtuso em B, onde IG é paralelo BC, sendo I o incentro e G o baricentro do triângulo. Sabendo-se que o perímetro do triângulo ABC é 144. Calcular o máximo valor inteiro de IG.
a)4
b)5
c)6
d)3
e)7
R:E

Eu comecei a rascunhar aqui e, por geometria analítica, descobri que o lado oposto ao vértice B é 48 e o valor de IG é dado por (48-c)/3, com C sendo o lado oposto ao vértice C. O macete é usar as desigualdades dos lados e descobrir qual será o menor C de modo que satisfaça o problema.

Vamos considerar esse triangulo no plano cartesiano:

Eu fixei o vértice A na origem do plano, e chamei os lados estão conforme os ângulos opostos a eles.

Sendo assim, temos que:

O Incentro pode ser escrito da forma :

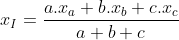
e


e o Baricentro pode ser escrito como:

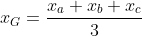
e


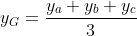
Substituindo os valores dos pontos A, B e C.

A:(0,0)
B:(Xb,Yb)
C:(b,0)

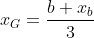(i)

(ii)

(iii)

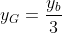(iiii)

Como o segmento IG é paralelo a base AC, o valor do eixo y deverá ser igual para os dois. ( Pelo fato de AC estar na abscissa)

Então,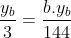  

b=48

Vamos analisar o valor do segmento IG :

Sabemos que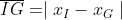  

Substituindo as igualdades (i), (ii), (iii) e (iiii) descobriremos que:



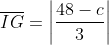
Analisando o triangulo pelas desigualdades, teremos que 48 > c > 24 (vamos lembrar que a+b+c=144 e que b=48) e, portanto, .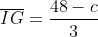

Agora para IG máximo, c terá que ser mínimo e múltiplo de 3 (IG é inteiro).

Analisando a desigualdade, c deverá ser 27 e com isso IG 21/3=7 .

Qualquer duvida só perguntar

Valeu renan2014!
Analítica é uma bela ferramenta para dar um balãozinho na plana..