PA - Determine

por RamonLucas Qua 05 Jul 2017, 10:49

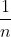(UFRJ) Para cada número natural $n\geqslant 1$ , seja Fn a figura plana composta de quadrinhos de lados iguais a $\frac{1}{n}$ , disposto da seguinte forma:

F_n é formada por uma fila de n quadrinhos, mais uma fila de ( n- 1) quadrinhos, mais uma fola de ( n - 2 ) quadrinhos e assim sucessivamente, sendo a última fila composta de um só quadrinho ( a figura ilustra o cado n = 7). Calcule o limite da área de F_n quando n tende a infinito.

Gabarito: 1/ 2

por **petras** Qua 05 Jul 2017, 10:57

A = [n + (n - 1) + (n - 2) + (n - 3) + ... + 2 + 1] ∙ 1/n²

mas [n + (n - 1) + (n - 2) + (n - 3) + ... + 2 + 1] corresponde à soma dos "n" termos de uma P.A. de razão r = 1.

A = (1 + n) ∙ (n/2) ∙ (1/n²)

A = (1 + n)/(2n)

A = (1/2n) + 1/2 (essa é a área da figura)

Então, quando "n" tende ao infinito, ou seja, n → ∞, temos que:

(1/2n) → 0, ou seja, (1/2n) tende à zero. portanto A = 0+1/2 = 1/2

PA - Determine

PA - Determine

Re: PA - Determine

Um fórum livre e democrático.