Números complexos
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
fantecele- Fera

- Mensagens : 1225
Data de inscrição : 14/09/2014
Idade : 27
Localização : Nova Venécia-ES, Brasil
 Re: Números complexos
Re: Números complexos
Obrigado pela resolução.
Por estar afastado dos estudos a alguns meses, ainda possuo algumas dificuldades. Tenho noção que cis(θ) representa a forma trigonométrica (cos(θ)+isen(θ)), mas ainda não consegui entender sua resolução.
Dúvidas:
-Sendo z8 = 1, isso implica que o módulo de z é 1? Se sim, por quê?
-Baseado em que, pode-se afirmar que θ=2πk/8?
-Por que k=3?
Por estar afastado dos estudos a alguns meses, ainda possuo algumas dificuldades. Tenho noção que cis(θ) representa a forma trigonométrica (cos(θ)+isen(θ)), mas ainda não consegui entender sua resolução.
Dúvidas:
-Sendo z8 = 1, isso implica que o módulo de z é 1? Se sim, por quê?
-Baseado em que, pode-se afirmar que θ=2πk/8?
-Por que k=3?
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
 Re: Números complexos
Re: Números complexos
-Sendo z8 = 1, isso implica que o módulo de z é 1? Se sim, por quê?
Sim. É fácil perceber que |z8| = 1, sendo |zn| = |z|n, temos que |z8| = |z|8 = 1. O módulo de um número complexo dever ser real e positivo, dessa forma se |z|8 = 1 →![|z| = \sqrt[8]{1}](https://latex.codecogs.com/gif.latex?|z|&space;=&space;\sqrt[8]{1}) , necessariamente |z| é igual a 1.
, necessariamente |z| é igual a 1.
-Baseado em que, pode-se afirmar que θ=2πk/8?
Segunda lei de Moivre:
![\\\sqrt[n]{z}=\sqrt[n]{|z|}.\left ( cos\left ( \frac{\theta+2k\pi}{n} \right )+i.sen\left ( \frac{\theta+2k\pi}{8} \right ) \right)](https://latex.codecogs.com/gif.latex?\\\sqrt[n]{z}=\sqrt[n]{|z|}.\left&space;(&space;cos\left&space;(&space;\frac{\theta+2k\pi}{n}&space;\right&space;)+i.sen\left&space;(&space;\frac{\theta+2k\pi}{8}&space;\right&space;)&space;\right))
z8 = 1
z8 = cos(0)
z8 = cis(0)
Utilizando a segunda lei de Moivre, sendo "θ" = 0 e |z8| = 1:
![\\\sqrt[8]{z^8}=\sqrt[8]{|1|}.\left ( cos\left ( \frac{0+2k\pi}{8} \right )+i.sen\left ( \frac{0+2k\pi}{8} \right ) \right)\\z=cis\left ( \frac{2k\pi}{8} \right )](https://latex.codecogs.com/gif.latex?\\\sqrt[8]{z^8}=\sqrt[8]{|1|}.\left&space;(&space;cos\left&space;(&space;\frac{0+2k\pi}{8}&space;\right&space;)+i.sen\left&space;(&space;\frac{0+2k\pi}{8}&space;\right&space;)&space;\right)\\z=cis\left&space;(&space;\frac{2k\pi}{8}&space;\right&space;))
k = 0; 1; 2; ...; 7.
-Por que k=3?
Temos que+isen(\alpha))) , dessa forma:
, dessa forma:
=\frac{x}{\sqrt{x^2+y^2}};sen(\alpha)=\frac{y}{\sqrt{x^2+y^2}})
Obviamente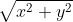 é positivo.
é positivo.
Do enunciado temos que x < 0 < y, portanto o cosseno deve ser negativo e o seno positivo.
De;k=0;1;2;...;7.) , vemos que o único valor que satisfaz a condição do seno e do cosseno acima é para quando temos k = 3.
, vemos que o único valor que satisfaz a condição do seno e do cosseno acima é para quando temos k = 3.
Sim. É fácil perceber que |z8| = 1, sendo |zn| = |z|n, temos que |z8| = |z|8 = 1. O módulo de um número complexo dever ser real e positivo, dessa forma se |z|8 = 1 →
-Baseado em que, pode-se afirmar que θ=2πk/8?
Segunda lei de Moivre:
z8 = 1
z8 = cos(0)
z8 = cis(0)
Utilizando a segunda lei de Moivre, sendo "θ" = 0 e |z8| = 1:
k = 0; 1; 2; ...; 7.
-Por que k=3?
Temos que
Obviamente
Do enunciado temos que x < 0 < y, portanto o cosseno deve ser negativo e o seno positivo.
De
fantecele- Fera

- Mensagens : 1225
Data de inscrição : 14/09/2014
Idade : 27
Localização : Nova Venécia-ES, Brasil
 Re: Números complexos
Re: Números complexos
z8 = 1
z8 = cos(0)
z8 = cis(0)
Nessa parte usa o cosseno como base porque o valor de z8 é real, não é?
z8 = cos(0)
z8 = cis(0)
Nessa parte usa o cosseno como base porque o valor de z8 é real, não é?
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
 Re: Números complexos
Re: Números complexos
z8 sim, cos(0) = 1.
A ideia ali era colocar o z8 na forma trigonométrica (z8 = cos(0) + i.sen(0)), acabei esquecendo do "i.sen(0)", porém não faz muita diferença, já que sen(0) = 0.
A ideia ali era colocar o z8 na forma trigonométrica (z8 = cos(0) + i.sen(0)), acabei esquecendo do "i.sen(0)", porém não faz muita diferença, já que sen(0) = 0.
fantecele- Fera

- Mensagens : 1225
Data de inscrição : 14/09/2014
Idade : 27
Localização : Nova Venécia-ES, Brasil
 Re: Números complexos
Re: Números complexos
Valeu!
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












