Trabalho da força de atrito
2 participantes
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
 Trabalho da força de atrito
Trabalho da força de atrito
Uma caixa de 547,9 N é empurrada para cima ao longo de um plano inclinado de 9 m de comprimento. São necessários 3,1 kJ para levar a caixa até o topo do plano, que está a 1,2 m acima da base. Qual é o módulo da força de atrito média que age sobre o bloco? (suponha que a caixa parte do repouso e chega ao topo do plano com velocidade nula).
Eu entendo que através das medidas da rampa podemos achar o ângulo de inclinação e posteriormente calcular a componente x do peso. Desta maneira a força resultante seria a diferença da força exercida sobre a caixa pela soma das forças de atrito e da componente x do peso. Entretanto, como posso achar a força de atrito neste caso? Não consigo relacionar o trabalho com o problema.
Eu entendo que através das medidas da rampa podemos achar o ângulo de inclinação e posteriormente calcular a componente x do peso. Desta maneira a força resultante seria a diferença da força exercida sobre a caixa pela soma das forças de atrito e da componente x do peso. Entretanto, como posso achar a força de atrito neste caso? Não consigo relacionar o trabalho com o problema.
vincent12- Padawan

- Mensagens : 59
Data de inscrição : 18/04/2017
Idade : 28
Localização : São Paulo
 Re: Trabalho da força de atrito
Re: Trabalho da força de atrito
O trabalho líquido necessário para elevar a caixa na ausência de atritos é (em módulo) W=mgh (547,9×1,2=657,48 J), igual ao trabalho do peso. Foram, porém, gastos 3100 J, o que significa que 2442,52 J foram dissipados pelo trabalho do atrito.
Assim, a força de atrito será 2442,52÷9=271,4 N
Se quisermos prosseguir numa verificação, vamos calcular o cosseno do ângulo
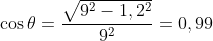
assim ao coeficiente de atrito será
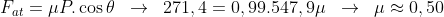
Assim, a força de atrito será 2442,52÷9=271,4 N
Se quisermos prosseguir numa verificação, vamos calcular o cosseno do ângulo
assim ao coeficiente de atrito será
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Tópicos semelhantes
Tópicos semelhantes» Trabalho e força de atrito
» TRABALHO DA FORÇA DE ATRITO
» Trabalho da força de atrito
» trabalho da força de atrito
» Trabalho da força de atrito
» TRABALHO DA FORÇA DE ATRITO
» Trabalho da força de atrito
» trabalho da força de atrito
» Trabalho da força de atrito
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












