Inequação modular

por Pedro 01 Sex 10 Fev 2017, 19:11

(ITA-91) Se $Inequação modular Gif$ , então temos:

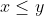A) $Inequação modular Gif$

B) $Inequação modular Gif$

C) $Inequação modular Gif$

D) $Inequação modular Gif$

E)n.d.a

Pessoal eu sei que se $Inequação modular Gif$ , $Inequação modular Gif$ e $Inequação modular Gif$ , mas nesse caso tem módulo nos dois lados, queria saber se a resolução é da mesma forma.

por PedroCunha Sex 10 Fev 2017, 19:13

Olá, Pedro.

É a mesma ideia, a única é diferença é você vai ter aplicar essa 'fórmula' duas vezes, resultando em 'quatro' casos a serem analisados.

Se precisar de ajuda é só avisar.

Grande abraço,
Pedro.

por Matemathiago Sex 10 Fev 2017, 19:14

Observe que a parábola da esquerda é positiva para qualquer x.

Daí, você pode eliminar o módulo do lado esquerdo e resolver do jeito que você já sabe!

por Pedro 01 Sex 10 Fev 2017, 19:55

Pedro acho que entendi, mas sera que daria quatro casos mesmo? Veja se é isso mesmo. Se |x|<|y| então os quatro casos seriam:

para x e y >0 --> x < y

para x e y <0 --> x > y

para x>0 e y<0 --> x < -y

para x<0 e y>0 --> x > -y

por Pedro 01 Sex 10 Fev 2017, 19:57

Entendi, então essa era a sacada da questao hahah. Valeu Matemathiago!!

por Matemathiago Sex 10 Fev 2017, 21:52

Pedro 01 escreveu:Entendi, então essa era a sacada da questao hahah. Valeu Matemathiago!!

Haha, disponha!!

cheers

por biologiaéchato Dom 24 Dez 2017, 10:40

Apenas confirmando, a correta é a alternativa (a), né?

por **Elcioschin** Dom 24 Dez 2017, 13:29

|x² + x + 1| ≤ |x² + 2.x - 3| ---> x² + x + 1 > 0 --->

x² + x + 1| ≤ |x² + 2.x - 3| ---> Temos duas possibilidades?

a) x² + x + 1| ≤ - (x² + 2.x - 3) ---> 2.x² + 3.x - 2 ≤ 0 ---> Raízes -2 e 1/2 ---> [-2, 1/2]

b) x² + x + 1| ≤ + (x² + 2.x - 3) ---> - x + 4 ≤ 0 ---> x ≥ 4 ---> [4, ∞[