Estatística

(UFBA) Em relação aos conhecimentos sobre medidas de posição e de distribuição, pode-se afirmar: 

01. Se dois conjuntos têm a mesma média aritmética, então têm a mesma variância. 

Não, pois a variância vai depender de outros dados que não serão os mesmos, eu entendi, mas é difícil explicar 

02. Se dois conjuntos têm o mesmo desvio-padrão, então têm a mesma variância.

Sim, pois o desvio padrão é a raiz quadrada da variância, logo, terá que ser igual. 

04. Se, em uma prova, a nota máxima equivale a 10, a média das notas é 6, e a mediana é 4, então o percentual de alunos com nota acima da média é maior que 50%. 

Não consegui fazer  :scratch:

08. Se, ao se retirar de um conjunto 3 elementos com valores iguais a 10,5, a média aritmética cai de 6,5 para 5,5, então o número original de elementos desse conjunto é 15.

Eu também não avancei nessa. :scratch:

16. Se a tabela indica a distribuição dos salários dos funcionários de determinada empresa e se são contratados dois novos funcionários com salário de R$ 605,00 cada um, então a variância da nova distribuição dos salários ficará maior que a anterior.



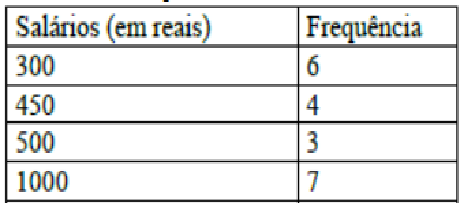
Essa aqui dá bastante cálculos, não sei se estou no caminho certo, 
primeiro pensei em achar a média:

x=[(300*6)+(450*4)+(500*3)+(1000*7)]/ nº funcionários

Só que eu não sei o nº funcionários, por isso não consegui calcular a variância.



Somatório das corretas: 26

08. Se, ao se retirar de um conjunto 3 elementos com valores iguais a 10,5, a média aritmética cai de 6,5 para 5,5, então o número original de elementos desse conjunto é 15.

Pelo o que eu entendi...

Tu precisas testar a afirmação da questao. Ele diz que a média original é 6,5 e o número de elementos é 15, logo tu precisas achar a somatória dos elementos.

Média = soma/15
6,5 = soma/15
soma = 97,5 (Essa é a soma dos valores dos 15 elementos originais)

Agora a jogada é raciocínio.. Se ele removeu do conjunto 3 valores, entao sao 15 - 3 = 12, concorda? Se cada valor removido vale 10,5, entao (10,5)*3 = 31,5, nao é?

Média = soma/15
Média = 97,5 - 31,5 / 15 - 3 (Aqui ele está removendo os elementos e seus valores)
Média = 66/12
Média = 5,5

Entao a afirmação tá certa.. Sao 15 elementos, pois a média nova bate com as condições.

16)Se a tabela indica a distribuição dos salários dos funcionários de determinada empresa e se são contratados dois novos funcionários com salário de R$ 605,00 cada um, então a variância da nova distribuição dos salários ficará maior que a anterior.

O número de funcionários é própria frequencia.. O 300 tem frequencia de 6, isso quer dizer que o 300 aparece 6 vezes na distribuição, logo sao 6 funcionários que recebem 300. O mesmo tu vai pensar pra todos os outros. O total de funcionários é a soma das frequencias, ou seja, 20.

Quando ele diz que dois novos funcionários foram contratados, cada um recebendo 605, isso é o mesmo que dizer que 605 aparecerá duas vezes como frequencia.

x=[(300*6)+(450*4)+(500*3)+(1000*7)]/ 20
x = 605

A nova média é:

x=[(300*6)+(450*4)+(500*3)+(1000*7) + (605*2)]/ 20 + 2 (dois novos funcionários)
x=[(300*6)+(450*4)+(500*3)+(1000*7)]/ 22
x= 605

A média é igual.

Agora, entendi, muito obrigada!!!

Só uma dúvida que fiquei na (16), a questão afirma que a variância da nova distribuição dos salários ficará maior que a anterior .

Como a média ficou igual, a variância para a nova distribuição do salário ficaria assim:

V= [(300-605)²+(450-605)²+(500-605)²+(1000-605)²+(605-605)²]/22

V=[(300-605)²+(450-605)²+(500-605)²+(1000-605)²+(0)] /22

A primeira variância seria a mesma coisa, só que dividida pelos 20 funcionários, neh ? 

Então, como o denominador da variância por 22 é maior que o primeiro de 20 funcionários, dará o valor da variância pelos 22 funcionários um número menor, já que o denominador é maior. 

Portanto, a variância da nova distribuição dos salários não ficaria menor do que a primeira variância com somente 20 funcionários ?

 É que a questão disse como correta que seria maior, fiquei na dúvida  :suspect:

Só corrigindo, Luana..

Quando tu tiras a variância de valores que possuem frequencia, também precisas multiplicar o valor pela frequencia, pq esses valores aparecem mais de uma vez. No caso, ficaria:

V= [6*(300-605)² + 4*(450-605)² + 3*(500-605)² + 7*(1000-605)²] / 20 (haja munheca pra fazer no papel)

Se nao houvesse frequencia, entao nao precisarias multiplicar por nada, pois só aparecem uma vez mesmo, entao seria o mesmo que multiplicar cada número por 1, que dá ele mesmo.

Voltando a questao..

Fiz o cálculo da variancia com os dois novos funcionários e realmente, deu um valor menor do que a primeira variancia com 20 funcionários. Ou o gabarito tá errado ou a gente tá esquecendo alguma coisa...
:SW1:

Desculpa.. Agora só outra pessoa pra tirar essa dúvida minha também :geek: .

Ah sim, tudo bem