raiz de número complexo
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 raiz de número complexo
raiz de número complexo
Determine a raiz 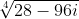 usando a definição de
usando a definição de 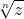

LeoZ- Jedi

- Mensagens : 200
Data de inscrição : 30/03/2015
Idade : 30
Localização : Rio de Janeiro
 Re: raiz de número complexo
Re: raiz de número complexo
Defina z=28-96i
Vamos colocá-lo na forma polar dos complexos:
Módulo:|z|=\sqrt{28^2+(-96)^2}=100
Argumento:\theta=\arctan{\frac{-96}{28}}
Assim:z=100cis(\theta)
\sqrt[4]{z}=\sqrt[4]{100}\;cis(\frac{\theta}{4})
Veja\cos{\theta}=\frac{28}{100} e \sin{\theta}=\frac{-96}{100} .
Então
\cos{\frac{\theta}{2}}=\sqrt{\frac{1+\cos{\theta}}{2}}=\frac{4}{5}\\ \cos{\frac{\theta}{4}}=\sqrt{\frac{1+\cos{\frac{\theta}{2}}}{2}}=\frac{3}{\sqrt{10}}
e
\sin{\frac{\theta}{2}}=\frac{\sin{\theta}}{2\cos{\frac{\theta}{2}}}=\frac{-3}{5}\\ \sin{\frac{\theta}{4}}=\frac{\sin{\frac{\theta}{2}}}{2\cos{\frac{\theta}{4}}}=\frac{\frac{-3}{5}}{2(\frac{3}{\sqrt{10}})}=\frac{-1}{\sqrt{10}}
Logo:
\sqrt[4]{z}=\sqrt{10}(\frac{3}{\sqrt{10}}-i\frac{1}{\sqrt{10}})=3-i
Qualquer dúvida com as transformações trigonométricas que fiz, ou outra coisa, pergunta aí. Espero ter ajudado, abraço!
Vamos colocá-lo na forma polar dos complexos:
Módulo:
Argumento:
Assim:
Veja
Então
e
Logo:
Qualquer dúvida com as transformações trigonométricas que fiz, ou outra coisa, pergunta aí. Espero ter ajudado, abraço!

gabrieldpb- Fera

- Mensagens : 284
Data de inscrição : 08/02/2016
Idade : 29
Localização : Ribeirão Preto
 Re: raiz de número complexo
Re: raiz de número complexo
Boa tarde, Gabriel!
Li sua ótima resolução e achei bem interessante, mas o complexo dado também apresenta outras raízes, como -3+i. Há como encontrá-las por esse método ou ele permite apenas a "principal"?
Li sua ótima resolução e achei bem interessante, mas o complexo dado também apresenta outras raízes, como -3+i. Há como encontrá-las por esse método ou ele permite apenas a "principal"?

GFMCarvalho- Jedi

- Mensagens : 232
Data de inscrição : 03/10/2015
Idade : 24
Localização : Itajubá, Minas Gerais, Brasil
 Re: raiz de número complexo
Re: raiz de número complexo
Há sim, GFMCarvalho, pois eu omiti as demais raízes. O enunciado disse ache A raiz, e acabei me deixando influenciar, mas bem lembrado!
Na verdade, quando escrevemos z na forma polar, vemos que na verdade se somarmos (ou subtrairmos) múltiplos de2\pi no seu argumento, ainda continuaremos com o mesmo z - é só você desenhar no plano de Argand-Gauss e irá notar. Então, genericamente falando:
z=100\; cis(\theta+2\pi k) para k inteiro
\sqrt[4]{z}=\sqrt[4]{100}\; cis(\frac{\theta}{4}+\frac{2\pi k}{4})
Veja que podemos limitar k a 0,1,2 e 3, pois qualquer outros inteiros irão resultar em redundância, dado que por exemplo, se k=5
\frac{2\pi \cdot 5}{4} = \frac{2\pi \cdot 1}{4} + 2\pi
Logo, como múltiplos de 2pi geram o mesmo argumento, k=5 gera a mesma raiz que k=1.
Logo, as outras raizes ficam determinadas por:
z_0=\sqrt{10}\; cis(\theta)=3-i para k=0
z_1=\sqrt{10}\; cis(\frac{\theta}{4} + \frac{\pi}{2}) para k=1
z_2=\sqrt{10}\; cis(\frac{\theta}{4} + \pi) para k=2
z_3=\sqrt{10}\; cis(\frac{\theta}{4} + \frac{3\pi}{2}) para k=3
Logo,
z_1=\sqrt{10}(\cos{(\frac{\theta}{4} + \frac{\pi}{2})}+i\sin{(\frac{\theta}{4} + \frac{\pi}{2})})\\ z_1=\sqrt{10}(-\sin{\frac{\theta}{4}}+i\cos{\frac{\theta}{4}})=1+3i
z_2=\sqrt{10}(\cos{(\frac{\theta}{4} + \pi)}+i\sin{(\frac{\theta}{4} + \pi)})\\ z_2=-\sqrt{10}(\cos{\frac{\theta}{4}}+i\sin{\frac{\theta}{4}})=-3+i
z_3=\sqrt{10}(\cos(\frac{\theta}{4} + \frac{3\pi}{2})+i\sin{(\frac{\theta}{4} + \frac{3\pi}{2}}))\\ z_3=-\sqrt{10}(-\sin{\frac{\theta}{4}}+i\cos{\frac{\theta}{4}})=-1-3i
Abraço!
Na verdade, quando escrevemos z na forma polar, vemos que na verdade se somarmos (ou subtrairmos) múltiplos de
Veja que podemos limitar k a 0,1,2 e 3, pois qualquer outros inteiros irão resultar em redundância, dado que por exemplo, se k=5
Logo, como múltiplos de 2pi geram o mesmo argumento, k=5 gera a mesma raiz que k=1.
Logo, as outras raizes ficam determinadas por:
Logo,
Abraço!

gabrieldpb- Fera

- Mensagens : 284
Data de inscrição : 08/02/2016
Idade : 29
Localização : Ribeirão Preto
 Re: raiz de número complexo
Re: raiz de número complexo
Ah, sim! Muito obrigado!
Agora que fui notar que você usou a fórmula de De Moivre, mas com a notação cis, hehehe.
Agora que fui notar que você usou a fórmula de De Moivre, mas com a notação cis, hehehe.

GFMCarvalho- Jedi

- Mensagens : 232
Data de inscrição : 03/10/2015
Idade : 24
Localização : Itajubá, Minas Gerais, Brasil

gabrieldpb- Fera

- Mensagens : 284
Data de inscrição : 08/02/2016
Idade : 29
Localização : Ribeirão Preto
 Re: raiz de número complexo
Re: raiz de número complexo
Tinha travado em senθ=-96/100 e cosθ=28/100 . Muito bom esse lance das relações trigonométricas. Show!
EsdrasCFOPM- Estrela Dourada

- Mensagens : 1247
Data de inscrição : 22/02/2016
Idade : 30
Localização : Salvador, Bahia, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Raiz de um número complexo
» Raiz de Numero Complexo
» Raiz de número complexo
» Raiz do número complexo (trigonométrica)
» Raiz quadrada de um número complexo
» Raiz de Numero Complexo
» Raiz de número complexo
» Raiz do número complexo (trigonométrica)
» Raiz quadrada de um número complexo
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












