Crescimento/decrescimento - Máx. e Mín.

Encontre os intervalos de crescimento e de decrescimento, os máximos e os mínimos da função:



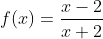
Obrigado

Para x diferente de -2, derivemos a função:

f'(x)=\frac{(x+2)-(x-2)}{(x+2)^2}=\frac{4}{(x+2)^2}

Candidatos a ponto de máximo/mínimo são aqueles o qual f'(x)=0
Nesse caso nenhum ponto satisfaz condição de máximo/mínimo

Calculemos a segunda derivada:

f''(x)=\frac{-4(2)(x+2)}{(x+2)^4}=\frac{-8}{(x+2)^3}

Antes da análise em si, veja que quando x tende ao (-) infinito ou (+) infinito, f(x) tende a 1. Do mesmo modo que para x tendendo a -2 pela esquerda, f(x) tende (+) infinito; para x tendendo a -2 pela direita, f(x) tende para (-) infinito. Ou seja, temos uma assintota horizontal (y=1) e uma assintota vertical (x=-2).

Quando x vem de - inf. para -2, pela derivada ser positiva em todo o trecho, f(x) será estritamente crescente, no intervalo ]-inf,-2[.

Do mesmo modo, quando x sai de -2 para + inf, f(x) sai de -inf para voltar a "caminhar" para 1, novamente, de forma estritamente crescente nesse intervalo ]-2,+inf[.

Resumindo, a função não é definida em -2, tem duas assintotas - vertical (x=-2) e horizontal (y=1) - e é crescente o tempo todo. É estritamente crescente apenas nos intervalos considerados e não admite nenhum ponto de máximo/mínimo.

Abraço!

Obrigado parceiro