Progressão Aritmética e Geométrica

A sequência (8, 19, ...) é obtida somando-se os termos correspondentes de duas progressões: uma aritmética (P A) e
outra geométrica (PG), de razões iguais.
O primeiro termo 8 é o resultado da soma do primeirotermo da PA com o primeiro termo da PG; o segundo termo19
é o resultado da soma do segundo termo da PA com o segundo termo da PG, e assim sucessivamente.
Sabendo-se que o primeiro termo da PA é igual ao primeiro termo da PG, podemos calcular o quinto termoda sequência
(8, 19, ...), igual a:
a) 330
b) 280
c) 340
d) 290

R: c



Eu chego que o primeiro termo, x, é igual a 4 e 

r + 4q = 15

r + q^4 = (W - 4)/4 sendo W o quinto termo da sequência


E travo...

a - r , a , a + r  ---> PA

q/r , q , qr        ---> PG

relações tiradas do enunciado:  



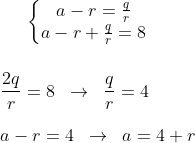
substituindo na sequência:

4 , 4 + r , 4 + 2r  ---> PA

4 , 4r , 4r²         ----> PG

do segundo termo: 4 + r + 4r = 19 --> 5r = 15  --> r = 3

quinto termo da PA: 

quinto termo da PG: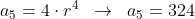 

a soma destes compõem o quinto da sequência: 324 + 16 = 340