Velocidade vetorial

Considere um carro A dirigindo-se para o Norte, com velocidade vA de intensidade igual a 45 km/h, e um carro B dirigindo-se para o Leste, com velocidade vB de intensidade igual a 60 km/h, conforme representa a figura a seguir:



Aponte a alternativa que melhor traduz as características da velocidade vBa do carro B em relação ao carro A:

Gab: C


Pelo tópicos de física, consta como solução a seguinte equação através da velocidade relativa: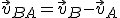 . Não consegui compreender esse raciocínio, visto que por estarem em perpendicular,  vejo como única solução o uso do teorema de Pitágoras para achar a Velocidade relativa dos carros (75km/h). Além do mais, gostaria de entender o porquê o ângulo da velocidade relativa ficar menor que 45°.

Giovana Martins escreveu:

De fato, vamos utilizar o Teorema de Pitágoras, mas do conceito de velocidade relativa você consegue entender a ideia da subtração, certo?

Bom, o sinal negativo atrelado a velocidade do corpo A, no momento do cálculo vetorial, fará com que o sentido (a direção se mantém) da representação da velocidade vetorial de A sofra uma inversão, daí vem a representação vetorial a seguir:



Nota¹: cada quadrado representa 15 km/h.

A própria representação vetorial, feita em escala, deixa bem indicado que θ < 45°.

\\tg(\theta )=\frac{45}{60}\to tg(\theta )=\frac{3}{4}\neq 1\ \therefore \ \theta \neq 45^{\circ}

Nota²: o ângulo seria de 45° se as velocidade de ambos os corpos fossem iguais.

Cálculo da velocidade do corpo B em relação ao corpo A:

v_{B,A}=\sqrt{(45)^2+(60)^2}\to \boxed {v_{B,A}=75\ \frac{km}{h}}

Consegui entender o θ < 45°, porém ainda não "peguei" a ideia da velocidade relativa. Sei que em sentidos opostos, as velocidades são somadas, e no mesmo sentido, subtraídas, porém, em meus livros só existe esse exemplo no eixo horizontal. Com o movimento perpendicular dos carros, não ficou claro essa idéia do vetor A ficar negativo.

Neste caso não existem "mesmo sentido" e "sentidos opostos"

Vba = Vb - Va ---> Vba = Vb + (-Va) ---> soma de Vb com o inverso de Va

Basta inverter Va e somar com Vb ---> Para o valor da resultante, use Pitágoras

Elcioschin escreveu:Neste caso não existem "mesmo sentido" e "sentidos opostos"

Vba = Vb - Va ---> Vba = Vb + (-Va) ---> soma de Vb com o inverso de Va

Basta inverter Va e somar com Vb ---> Para o valor da resultante, use Pitágoras

Beleza, obrigado pelas respostas, consegui entender.

A inversão é devido ao fato de você ter um escalar negativo multiplicando um vetor. É uma propriedade das operações vetoriais.