Volume do tanque
4 participantes
Página 1 de 1
Volume do tanque
por Pietro di Bernadone Qui 29 Jul 2010, 11:11
Bom dia prezados usuários do Pir²!
Um tanque de uso industrial tem a forma de um prisma cuja base é um trapézio isósceles. Na figura abaixo, são dadas as dimensões (em metros) do prisma. O volume desse tanque em m³ é:
a) 50
b) 60
c) 80
d) 100
e) 120
Certo de sua atenção,
Pietro di Bernadone
Um tanque de uso industrial tem a forma de um prisma cuja base é um trapézio isósceles. Na figura abaixo, são dadas as dimensões (em metros) do prisma. O volume desse tanque em m³ é:
a) 50
b) 60
c) 80
d) 100
e) 120
Certo de sua atenção,
Pietro di Bernadone
Pietro di Bernadone- Grupo
Velhos amigos do Fórum
- Mensagens : 1344
Data de inscrição : 04/03/2010
Idade : 34
Localização : Rio de Janeiro
Re: Volume do tanque
por Elcioschin Qui 29 Jul 2010, 11:23
Altura do trapézio ----> h² = 5² - 3² ----> h = 4 m
Área do trapésio (base do prisma)
S = (B + b)*h/2 ----> S = (8 + 2)*4/2 ----> S = 20 m²
V = S*H ----> V = 20*5 ----> V = 100 m³
Área do trapésio (base do prisma)
S = (B + b)*h/2 ----> S = (8 + 2)*4/2 ----> S = 20 m²
V = S*H ----> V = 20*5 ----> V = 100 m³
Elcioschin- Grande Mestre
- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: Volume do tanque
por Pietro di Bernadone Qui 29 Jul 2010, 12:08
Elcio,
não consegui entender como foi calculada a altura do trapézio. Qual fórmula foi usada?
Certo de sua atenção,
Pietro di Bernadone
não consegui entender como foi calculada a altura do trapézio. Qual fórmula foi usada?
Certo de sua atenção,
Pietro di Bernadone
Pietro di Bernadone- Grupo
Velhos amigos do Fórum - Mensagens : 1344
Data de inscrição : 04/03/2010
Idade : 34
Localização : Rio de Janeiro
Re: Volume do tanque
por Euclides Qui 29 Jul 2010, 13:34
Olá Pietro, procure não se prender a "fórmulas" para tudo. Em Geometria é preciso dominar bem as relações básicas (triângulos retângulos e Pitágoras é fundamental) e fragmentar a figura em figuras fundamentais fáceis de calcular com os elementos básicos da geometria:
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.
Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.
Euclides- Fundador
- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
Re: Volume do tanque
por Pietro di Bernadone Qui 29 Jul 2010, 15:32
Opa! A ilustração ficou excelente e facilitou a interpretação! Foi aplicado o Teorema de Pitágoras no triângulo amarelo para encontrar a altura.
Obrigado Euclides e Elcio pela excelente resolução do problema.
Atenciosamente,
Pietro di Bernadone
Obrigado Euclides e Elcio pela excelente resolução do problema.
Atenciosamente,
Pietro di Bernadone
Pietro di Bernadone- Grupo
Velhos amigos do Fórum - Mensagens : 1344
Data de inscrição : 04/03/2010
Idade : 34
Localização : Rio de Janeiro
Re: Volume do tanque
por Luan Henrique Silva Melo Sex 09 Set 2016, 19:36
O volume de um prisma é o produto da área da base pela altura!
A área da base é a área de um trapézio de base maior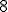
, base menor 
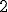e altura 
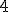. Logo, pela fórmula da área de um trapézio:
}{2}h=\frac{(8+2)}{2}4=20)
A área da base do prisma vale: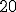
A altura do prisma é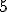
, como indicado na figura!
Então o volume é: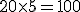
A área da base é a área de um trapézio de base maior
A área da base do prisma vale:
A altura do prisma é
Então o volume é:
Luan Henrique Silva Melo- Jedi
- Mensagens : 348
Data de inscrição : 29/06/2016
Idade : 26
Localização : Lages/SC
Tópicos semelhantes» Volume de um Tanque
» Volume de um tanque
» Volume Cubo em relação ao Volume Cilindro
» Volume do tanque cilíndrico
» Volume te um tanque Cilíndrico!
» Volume de um tanque
» Volume Cubo em relação ao Volume Cilindro
» Volume do tanque cilíndrico
» Volume te um tanque Cilíndrico!
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
