Álgebra Linear- Vetores LD e LI
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Álgebra Linear- Vetores LD e LI
por Huovi Ter 21 Out 2014, 10:38
Eu realmente estou me complicando um pouco com essas questões :s basicamente, tenho que:
a) Encontrar o valor de k para que os vetores u=(2 , 3) e v=(4 , k) sejam Linearmente Dependentes
b) Encontrar o valor de k para que os vetores u=(k, 1, 0), v=(2, 2, 3) e w=(-1, 0, 2) sejam Linearmente Independentes
Até a parte de determinar se é LD ou LI eu consegui resolver outros exercícios. Porém a presença desse k aí fez meu sistema ficar um pouco confuso, acho que os resultados aos quais cheguei não estão corretos :s e não tenho o gabarito para afirmar se está correto ou não :/ alguém conseguiu resolver?
Obrigada a todos pela atenção ^^
a) Encontrar o valor de k para que os vetores u=(2 , 3) e v=(4 , k) sejam Linearmente Dependentes
b) Encontrar o valor de k para que os vetores u=(k, 1, 0), v=(2, 2, 3) e w=(-1, 0, 2) sejam Linearmente Independentes
Até a parte de determinar se é LD ou LI eu consegui resolver outros exercícios. Porém a presença desse k aí fez meu sistema ficar um pouco confuso, acho que os resultados aos quais cheguei não estão corretos :s e não tenho o gabarito para afirmar se está correto ou não :/ alguém conseguiu resolver?
Obrigada a todos pela atenção ^^
Huovi- Iniciante
- Mensagens : 1
Data de inscrição : 21/10/2014
Idade : 28
Localização : Recife
Re: Álgebra Linear- Vetores LD e LI
por Carlos Adir Ter 21 Out 2014, 11:00
Você sabe o que é linearmente dependentes ou independentes?
Um vetor é linearmente independente de outro se os dois forem perpendiculares entre si.
Sejam os vetores:
;&space;\&space;\&space;\&space;w=(a_2,b_2) "u=(a_1,b_1); \ \ \ w=(a_2,b_2)")
O vetor resultante da soma desses dois é:
 "u+w = (a_1+a_2, b_1+b_2)")
Podemos então, aplicar pitágoras, se e somente se u e w forem perpendiculares entre si. Ou seja:
^2+(b_1+b_2)^2} "\\ |u| = \sqrt{a_1^2+b_1^2} \\ |w| = \sqrt{a_2^2+b_2^2}\\|u+w| = \sqrt{(a_1+a_2)^2+(b_1+b_2)^2}")
Se |u+w| é a hipotenusa, |u| é um cateto, e |w| é o outro, então:
^2+\left(&space;\sqrt{a_2^2+b_2^2}\right)^2=\left(\sqrt{(a_1+a_2)^2+(b_1+b_2)^2}\right)^2\\a_1^2+b_1^2+a_2^2+b_2^2=(a_1+a_2)^2+(b_1+b_2)^2\\&space;a_1^2+a_2^2+b_1^2+b_2^2=a_1^2+2a_1a_2+a_2^2+b_1^2+2b_1b_2+b_2^2\\2a_1a_2+2b_1b_2=0\\a_1a_2+b_1b_2=0 "\\ |u|^2+|w|^2 = |u+w|^2\\\left(\sqrt{a_1^2+b_1^2}\right)^2+\left( \sqrt{a_2^2+b_2^2}\right)^2=\left(\sqrt{(a_1+a_2)^2+(b_1+b_2)^2}\right)^2\\a_1^2+b_1^2+a_2^2+b_2^2=(a_1+a_2)^2+(b_1+b_2)^2\\ a_1^2+a_2^2+b_1^2+b_2^2=a_1^2+2a_1a_2+a_2^2+b_1^2+2b_1b_2+b_2^2\\2a_1a_2+2b_1b_2=0\\a_1a_2+b_1b_2=0")
Portanto, dois vetores são perpendiculares entre si se suas coordenadas satisfazerem a condição:
No espaço não muda, é o mesmo raciocinio. No fim, 3 vetores são linearmente independentes entre si se satisfazerem a condição:
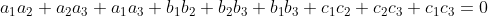
Assim:
a)Para k ser linearmente independente, k=(-
/3. Então para ser linearmente dependente, k =/= (-/3
b)Para k ser linearmente independente, k=(-6)
Um vetor é linearmente independente de outro se os dois forem perpendiculares entre si.
Sejam os vetores:
O vetor resultante da soma desses dois é:
Podemos então, aplicar pitágoras, se e somente se u e w forem perpendiculares entre si. Ou seja:
Se |u+w| é a hipotenusa, |u| é um cateto, e |w| é o outro, então:
Portanto, dois vetores são perpendiculares entre si se suas coordenadas satisfazerem a condição:
No espaço não muda, é o mesmo raciocinio. No fim, 3 vetores são linearmente independentes entre si se satisfazerem a condição:
Assim:
a)Para k ser linearmente independente, k=(-
/3. Então para ser linearmente dependente, k =/= (-/3b)Para k ser linearmente independente, k=(-6)
Carlos Adir- Monitor
- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
Tópicos semelhantes» Algebra Linear - Vetores
» Álgebra Linear - Vetores
» Seja T é uma aplicação linear de um espaço vetorial (Algebra Linear)
» 5.Ache uma aplicação linear T : R^4 --> R^3 (Algebra linear)
» Álgebra Linear - Vetores
» Álgebra Linear - Vetores
» Seja T é uma aplicação linear de um espaço vetorial (Algebra Linear)
» 5.Ache uma aplicação linear T : R^4 --> R^3 (Algebra linear)
» Álgebra Linear - Vetores
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
