EN 2008
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
EN 2008
por Falke Dom 31 Ago 2014, 12:36
Sejam n ∈ ℕ tal que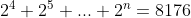 
e m o menor m ∈ ℕ tal que 
seja verdadeira. o produto m.n vale
(A) 120
(B) 124
(C) 130
(D) 132
(E) 143
(A) 120
(B) 124
(C) 130
(D) 132
(E) 143
Falke- Iniciante
- Mensagens : 24
Data de inscrição : 15/01/2013
Idade : 31
Localização : São paulo, SP
Re: EN 2008
por Ashitaka Dom 31 Ago 2014, 14:12
Motivo da edição: escrever de um jeito que considerei mais simples.
Última edição por Ashitaka em Dom 31 Ago 2014, 14:45, editado 3 vez(es)
Ashitaka- Monitor
- Mensagens : 4365
Data de inscrição : 12/03/2013
Localização : São Paulo
Re: EN 2008
por PedroCunha Dom 31 Ago 2014, 14:16
Olá.
2^4 + 2^5 + ... + 2^n = 8176 .:.
2¹ + 2² + 2³ + 2^4 + 2^5 + ... + 2^n = 8176 + 2¹ + 2² + 2³
[ 2 * (2^n - 1) ] / [ 2 - 1] = 8190 .:.
2^n - 1 = 4095 .:. 2^n = 4096 .:. n = 12
m!/(2*4*6*...(2m)) = m!/[ 2^m * (1 * 2 * 3 * ... * m) ]
= m!/[2^m*m!] = 1/2^m
Assim: 1/2^m <= 1/[6^{2log[6] 40}] .:. 1/2^m <= 1/[6^{log[6] 40²}] .:.
1/2^m <= 1/[40²] .:. 2^m >= (2³)² * 5² .:. 2^m <= 2^6 * 25 .:. m >= 11
Assim, o produto é 12*11 = 132
Att.,
Pedro
2^4 + 2^5 + ... + 2^n = 8176 .:.
2¹ + 2² + 2³ + 2^4 + 2^5 + ... + 2^n = 8176 + 2¹ + 2² + 2³
[ 2 * (2^n - 1) ] / [ 2 - 1] = 8190 .:.
2^n - 1 = 4095 .:. 2^n = 4096 .:. n = 12
m!/(2*4*6*...(2m)) = m!/[ 2^m * (1 * 2 * 3 * ... * m) ]
= m!/[2^m*m!] = 1/2^m
Assim: 1/2^m <= 1/[6^{2log[6] 40}] .:. 1/2^m <= 1/[6^{log[6] 40²}] .:.
1/2^m <= 1/[40²] .:. 2^m >= (2³)² * 5² .:. 2^m <= 2^6 * 25 .:. m >= 11
Assim, o produto é 12*11 = 132
Att.,
Pedro
PedroCunha- Monitor
- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
