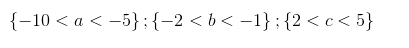Inequações Lineares II
2 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Re: Inequações Lineares II
Re: Inequações Lineares II
Olá, Luiz.
\\ -10 < a < -5 \therefore -10 \cdot (-2) > ab > -5 \cdot (-1) \therefore \frac{5}{5} < \frac{ab}{c} < \frac{20}{2} \\\\ \Leftrightarrow \boxed{\boxed{ 1 < \frac{ab}{c} < 10 }}
Que dá a alternativa e.
Penso que seja isso.
Abraços,
Pedro
Que dá a alternativa e.
Penso que seja isso.
Abraços,
Pedro

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: Inequações Lineares II
Re: Inequações Lineares II
Pedro, eu cheguei a fazer isso. Mas só um detalhe, a alternativa "e" é o intervalo (0;10), nós encontramos (1;10).
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Re: Inequações Lineares II
Re: Inequações Lineares II
Sim, mas o enunciado fala: "está contido".
(1;10) está contido em (0;10).
(1;10) está contido em (0;10).

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: Inequações Lineares II
Re: Inequações Lineares II
ah, é verdade. Valeu Pedro!
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Tópicos semelhantes
Tópicos semelhantes» Inequações Lineares
» Inequações Lineares III
» Inequações Lineares IV
» Inequações Lineares V
» Inequações de 2º grau e Inequações Produto
» Inequações Lineares III
» Inequações Lineares IV
» Inequações Lineares V
» Inequações de 2º grau e Inequações Produto
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos