Equação Trigonométrica de Rachar à Cuca
5 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
 Equação Trigonométrica de Rachar à Cuca
Equação Trigonométrica de Rachar à Cuca
Resolva a equação trigonométrica
tg(2x)+cotgx = 8cos²x
S={xeR/x=(∏/2)+k∏ ou x=(5∏/24)+(k∏/2) ou x= (∏/24)+(k∏/2) ,kez}
tranformando tudo em tg (x) eu caio nessa equação :(tgx)^4+8(tgx)^3+2(tgx)^2-8tgx+1 = 0
o que está me deixando muito confuso é o gabarito, como que x=(∏/2)+k∏ é uma das soluções se a condição de existência de tg(x) é justamente x≠ (∏/2)+k∏. E realmente x=(∏/2)+k∏ é solução pois testando na equação original a igualdade é comprovada.
Eu tenho uma explicação, mas gostaria de saber a de vocês também .
Valeu.
tg(2x)+cotgx = 8cos²x
S={xeR/x=(∏/2)+k∏ ou x=(5∏/24)+(k∏/2) ou x= (∏/24)+(k∏/2) ,kez}
tranformando tudo em tg (x) eu caio nessa equação :(tgx)^4+8(tgx)^3+2(tgx)^2-8tgx+1 = 0
o que está me deixando muito confuso é o gabarito, como que x=(∏/2)+k∏ é uma das soluções se a condição de existência de tg(x) é justamente x≠ (∏/2)+k∏. E realmente x=(∏/2)+k∏ é solução pois testando na equação original a igualdade é comprovada.
Eu tenho uma explicação, mas gostaria de saber a de vocês também .
Valeu.
Felipemqs- Iniciante
- Mensagens : 42
Data de inscrição : 10/06/2014
Idade : 30
Localização : SP
 Re: Equação Trigonométrica de Rachar à Cuca
Re: Equação Trigonométrica de Rachar à Cuca
Encontrei essa equação na internet como tg(2x) = 8cotg²x - cotgx.
Será que a sua equação está certa?
Será que a sua equação está certa?

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: Equação Trigonométrica de Rachar à Cuca
Re: Equação Trigonométrica de Rachar à Cuca
Felipemqs escreveu:Resolva a equação trigonométrica
tg(2x)+cotgx = 8cos²x
S={xeR/x=(∏/2)+k∏ ou x=(5∏/24)+(k∏/2) ou x= (∏/24)+(k∏/2) ,kez}
tranformando tudo em tg (x) eu caio nessa equação :(tgx)^4+8(tgx)^3+2(tgx)^2-8tgx+1 = 0
o que está me deixando muito confuso é o gabarito, como que x=(∏/2)+k∏ é uma das soluções se a condição de existência de tg(x) é justamente x≠ (∏/2)+k∏. E realmente x=(∏/2)+k∏ é solução pois testando na equação original a igualdade é comprovada.
Eu tenho uma explicação, mas gostaria de saber a de vocês também .
Valeu.
Olá

Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
 Re: Equação Trigonométrica de Rachar à Cuca
Re: Equação Trigonométrica de Rachar à Cuca
Esse exercício é do livro do Aref. Concordo com você que (∏/2)só não pertence ao dominio de 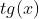 , mas pq deu esse erro , pois cai numa equação só com
, mas pq deu esse erro , pois cai numa equação só com 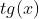 . como se deveria resolver essa questão então ?
. como se deveria resolver essa questão então ?
Felipemqs- Iniciante
- Mensagens : 42
Data de inscrição : 10/06/2014
Idade : 30
Localização : SP
 Re: Equação Trigonométrica de Rachar à Cuca
Re: Equação Trigonométrica de Rachar à Cuca
Quando você, por exemplo, eleva uma equação ao quadrado, você introduz raízes que NÃO atendem à equação original, ou raízes absurdas. Deve-se, sempre, testar as raízes na equação original, para ver quais delas atendem.
No seu caso, ao substituir, tg2x por 2.tgx/(1 - tg²x) você modificou perigosamente a equação original, chegando neste impasse a que você chegou.
Além disso, a função tgx não é definida para x = (2k + 1).pi/2
Logo, sua escolha de trabalhar com tgx foi uma infeliz escolha: tente trabalhar com senx e cosx que são funções contínuas e existem para qualquer valor de x
No seu caso, ao substituir, tg2x por 2.tgx/(1 - tg²x) você modificou perigosamente a equação original, chegando neste impasse a que você chegou.
Além disso, a função tgx não é definida para x = (2k + 1).pi/2
Logo, sua escolha de trabalhar com tgx foi uma infeliz escolha: tente trabalhar com senx e cosx que são funções contínuas e existem para qualquer valor de x

Elcioschin- Grande Mestre

- Mensagens : 73188
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Equação Trigonométrica de Rachar à Cuca
Re: Equação Trigonométrica de Rachar à Cuca
exatamente, ou poderia também trabalhar com cotgx pois ela está na equação original, e por isso não alteraria o domínio. colocando cotg x em evidência chego na seguinte equaçãoElcioschin escreveu:Quando você, por exemplo, eleva uma equação ao quadrado, você introduz raízes que NÃO atendem à equação original, ou raízes absurdas. Deve-se, sempre, testar as raízes na equação original, para ver quais delas atendem.
No seu caso, ao substituir, tg2x por 2.tgx/(1 - tg²x) você modificou perigosamente a equação original, chegando neste impasse a que você chegou.
Além disso, a função tgx não é definida para x = (2k + 1).pi/2
Logo, sua escolha de trabalhar com tgx foi uma infeliz escolha: tente trabalhar com senx e cosx que são funções contínuas e existem para qualquer valor de x
[cotgx[(cotgx^4)-8(cotgx^3)+2(cotgx^2)+8 cotgx +1]=0
cotg x =0 o resto eu não consigo desenvolver , alguém saberia como fazer ?
Felipemqs- Iniciante
- Mensagens : 42
Data de inscrição : 10/06/2014
Idade : 30
Localização : SP
 Re: Equação Trigonométrica de Rachar à Cuca
Re: Equação Trigonométrica de Rachar à Cuca
tg(2x) = 2.tgx/[1 - tg²x] = 2.(1/cotgx)/[1 - 1/cotg²x) = 2.cotgx/(cotg²x - 1)
cotg²x = cos²x/sen²x ---> cotg²x = cos²x/(1 - cos²x) ---> cotg²x - cotg²x.cos²x = cos²x --->
cotg²x = (1 + cotg²x).cos²x ---> cos²x = cotg²x/(cotg²x + 1)
Confira, faça cotgx = y (p/ facilitar), substitua e simplifique. Você chegará na equação: y.(ax^4 + bx² + cx) = 0
1ª raiz ---> y = 0 ---_> cotgx = 0 ----> x = pi/2 ou x = 3pi/2 (1ª volta) ----> x = kpi + pi/2
As outras 4 raízes você obtém da equação biquadrada (entre parênteses)
cotg²x = cos²x/sen²x ---> cotg²x = cos²x/(1 - cos²x) ---> cotg²x - cotg²x.cos²x = cos²x --->
cotg²x = (1 + cotg²x).cos²x ---> cos²x = cotg²x/(cotg²x + 1)
Confira, faça cotgx = y (p/ facilitar), substitua e simplifique. Você chegará na equação: y.(ax^4 + bx² + cx) = 0
1ª raiz ---> y = 0 ---_> cotgx = 0 ----> x = pi/2 ou x = 3pi/2 (1ª volta) ----> x = kpi + pi/2
As outras 4 raízes você obtém da equação biquadrada (entre parênteses)

Elcioschin- Grande Mestre

- Mensagens : 73188
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Equação Trigonométrica de Rachar à Cuca
Re: Equação Trigonométrica de Rachar à Cuca
Mas a equação é (cotgx^4)-8(cotgx^3)+2(cotgx^2)+8 cotgx +1 = 0Elcioschin escreveu:tg(2x) = 2.tgx/[1 - tg²x] = 2.(1/cotgx)/[1 - 1/cotg²x) = 2.cotgx/(cotg²x - 1)
cotg²x = cos²x/sen²x ---> cotg²x = cos²x/(1 - cos²x) ---> cotg²x - cotg²x.cos²x = cos²x --->
cotg²x = (1 + cotg²x).cos²x ---> cos²x = cotg²x/(cotg²x + 1)
Confira, faça cotgx = y (p/ facilitar), substitua e simplifique. Você chegará na equação: y.(ax^4 + bx² + cx) = 0
1ª raiz ---> y = 0 ---_> cotgx = 0 ----> x = pi/2 ou x = 3pi/2 (1ª volta) ----> x = kpi + pi/2
As outras 4 raízes você obtém da equação biquadrada (entre parênteses)
Felipemqs- Iniciante
- Mensagens : 42
Data de inscrição : 10/06/2014
Idade : 30
Localização : SP
 Re: Equação Trigonométrica de Rachar à Cuca
Re: Equação Trigonométrica de Rachar à Cuca
gente poderiam dizer ond estou errandoo no jeito q eu fiz? obg
(sen2x/cos2x) + (cosx/senx) = (sen2x.senx + cos2x.cosx)/cos2x.senx = 8cos²x, dai em cima fica cos x, cos x/cos2x.senx= 8cos²x
dai cosx = 8cos²x.cos2x.senx = 4.cosx.cos2x.(2.cosx.senx) = 4cosx.cos2x.sen2x = 2cosx.(2cos2x.sen2x) = 2cosx.sen4x = cosx
dai 2cosx.sen4x - cos x = o e cosx(2sen4x-1) = 0, e então cos x = 0 ou sen4x = 1/2
dai pra mim daria x = pi/2 + 2kpi ou x = pi/24 + kpi/2 ou x = 5pi/24 + kpi/2, mas a resposta do livro é (3pi+-2pi/24) + kpi/2
poderiam me ajudar, obrgado gente beiijos
(sen2x/cos2x) + (cosx/senx) = (sen2x.senx + cos2x.cosx)/cos2x.senx = 8cos²x, dai em cima fica cos x, cos x/cos2x.senx= 8cos²x
dai cosx = 8cos²x.cos2x.senx = 4.cosx.cos2x.(2.cosx.senx) = 4cosx.cos2x.sen2x = 2cosx.(2cos2x.sen2x) = 2cosx.sen4x = cosx
dai 2cosx.sen4x - cos x = o e cosx(2sen4x-1) = 0, e então cos x = 0 ou sen4x = 1/2
dai pra mim daria x = pi/2 + 2kpi ou x = pi/24 + kpi/2 ou x = 5pi/24 + kpi/2, mas a resposta do livro é (3pi+-2pi/24) + kpi/2
poderiam me ajudar, obrgado gente beiijos

Letícia Bittencourte- Padawan

- Mensagens : 94
Data de inscrição : 24/09/2014
Idade : 28
Localização : São Paulo, SP
 Tópicos semelhantes
Tópicos semelhantes» Equação trigonométrica
» Equação trigonométrica
» Equação trigonométrica - Equação simples
» Equação trigonométrica
» Equação trigonométrica
» Equação trigonométrica
» Equação trigonométrica - Equação simples
» Equação trigonométrica
» Equação trigonométrica
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












