Estudar uma série
2 participantes
Página 1 de 1
Estudar uma série
por marcoscastro87 Seg 31 maio 2010, 21:43
Olá pessoal, estou tendo algumas dificuldades para entender algumas coisas, aí vai a questão que vai me ajudar com certeza a resolver outras questões:
Estude a série:
autosoma de +infinito com k=1 de 1/(2k+1)
Seria de extrema valia a explicação dessa questão, pois irá ajudar e muito no entendimento de outras questões similares, valeu!
Estude a série:
autosoma de +infinito com k=1 de 1/(2k+1)
Seria de extrema valia a explicação dessa questão, pois irá ajudar e muito no entendimento de outras questões similares, valeu!
marcoscastro87- Padawan
- Mensagens : 90
Data de inscrição : 09/09/2009
Idade : 36
Localização : Teresina-Piauí
Re: Estudar uma série
por Euclides Ter 01 Jun 2010, 13:19
Olá Marcos, penso que para decidir sobre a convergência , ou não, dessa série o melhor é o teste da integral:
 \right )_1^{\infty}=\infty "\int_{1}^{\infty}\frac{dx}{2x+1}=\left (\frac{1}{2}ln(2x+1) \right )_1^{\infty}=\infty")
A série é divergente
A série é divergente
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.
Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.
Euclides- Fundador
- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
Re: Estudar uma série
por marcoscastro87 Qua 02 Jun 2010, 01:23
Olá Euclides, valeu pela resposta, mas tenho umas dúvidas, entendi como você chegou a expressão 1/2*ln(2x+1) e tudo mais, sei também que o limite de um logaritmo com base maior do que 1 que é o caso de ln, quando tende ao +infinito é +infinito, mas e no caso do limite inferior que é 1? Nesse caso desconsidera o limite inferior ? Pois eu me baseio pelo calculo de área que a gente tem limite superior menos o limite inferior e outra coisa, se for +infinito ou maior do que 1 é divergente e se for menor do que 1 é convergente é? Valeu
marcoscastro87- Padawan
- Mensagens : 90
Data de inscrição : 09/09/2009
Idade : 36
Localização : Teresina-Piauí
Re: Estudar uma série
por Euclides Qua 02 Jun 2010, 13:12
Ola Marcos:
"seja f uma função contínua, decrescente e de valores positivos para todo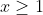
. Então a série infinita 
é convergente se a integral imprópria dx "\int_{1}^{\infty}f(x)dx")
existir. E será divergente de a integral imprópria crescer sem limite."
"seja f uma função contínua, decrescente e de valores positivos para todo
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.
Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.
Euclides- Fundador
- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
marcoscastro87- Padawan
- Mensagens : 90
Data de inscrição : 09/09/2009
Idade : 36
Localização : Teresina-Piauí
Tópicos semelhantes» Estudar uma série - verificar se a resolução está certa
» Estudar por livros ou então estudar com questões?
» ITA - livros para estudar e como estudar
» Como estudar calculo? Estudar pré-calculo antes ajuda?
» Estudar ou não?
» Estudar por livros ou então estudar com questões?
» ITA - livros para estudar e como estudar
» Como estudar calculo? Estudar pré-calculo antes ajuda?
» Estudar ou não?
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
