equação exponencial
3 participantes
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
 equação exponencial
equação exponencial
A soma dos valores reais de X que satisfazem a equação:
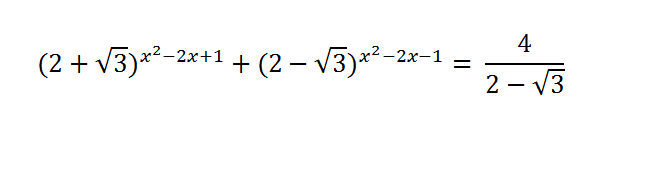
A resposta é 3
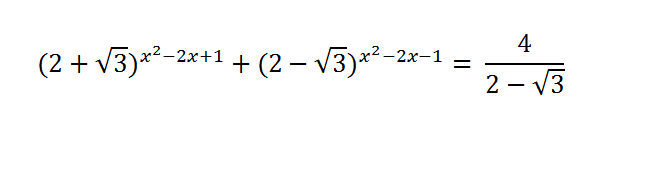
A resposta é 3
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Re: equação exponencial
Re: equação exponencial
Olá, luiz.bfg .
(2+√3)^{x²-2x+1} + (2-√3)^{x²-2x-1} = 4/(2-√3)
Mas veja que
1/(2+√3) = (2-√3)/(4-3) .:. 2-√3
Então: 2-√3 = (2+√3)^{-1}
Seja então y = 2+√3. Substituindo:
y^{x²-2x+1} + (y^{-1})^{x²-2x-1} = 4/(1/y) .:.
y^{x²-2x+1} + y^{-x²+2x+1} = 4y .:.
y^{x²-2x} * y + y^{-x²+2x} * y = 4y .:.
y^{x²-2x} + y^{-x²+2x} = 4 .:.
y^{x²-2x} + (y^{-1})^{x²-2x} = 4 .:.
y^{x²-2x} + 1/y^{x²-2x} = 4
Seja y^{x²-2x} = k, k > 0
k + 1/k = 4 .:. k² - 4k + 1 = 0 --> k = (4 +- √(12) ) /2 .:. k = 2 + √3
Então: y^{x²-2x} = 2+√3 .:. (2+√3)^{x²-2x} = (2+√3) --> x²-2x = 1 .:. x²-2x-1 = 0 .:. S = 2
O seu gabarito está errado. Os valores de x são 1-√2 e 1 + √2
Att.,
Pedro
(2+√3)^{x²-2x+1} + (2-√3)^{x²-2x-1} = 4/(2-√3)
Mas veja que
1/(2+√3) = (2-√3)/(4-3) .:. 2-√3
Então: 2-√3 = (2+√3)^{-1}
Seja então y = 2+√3. Substituindo:
y^{x²-2x+1} + (y^{-1})^{x²-2x-1} = 4/(1/y) .:.
y^{x²-2x+1} + y^{-x²+2x+1} = 4y .:.
y^{x²-2x} * y + y^{-x²+2x} * y = 4y .:.
y^{x²-2x} + y^{-x²+2x} = 4 .:.
y^{x²-2x} + (y^{-1})^{x²-2x} = 4 .:.
y^{x²-2x} + 1/y^{x²-2x} = 4
Seja y^{x²-2x} = k, k > 0
k + 1/k = 4 .:. k² - 4k + 1 = 0 --> k = (4 +- √(12) ) /2 .:. k = 2 + √3
Então: y^{x²-2x} = 2+√3 .:. (2+√3)^{x²-2x} = (2+√3) --> x²-2x = 1 .:. x²-2x-1 = 0 .:. S = 2
O seu gabarito está errado. Os valores de x são 1-√2 e 1 + √2
Att.,
Pedro

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: equação exponencial
Re: equação exponencial
valeu pedro!! deve estar mesmo
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Re: equação exponencial
Re: equação exponencial
pedro, voce pode me ajudar em mais uma questão?
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Re: equação exponencial
Re: equação exponencial
Claro, mas crie um topico para cada questão.

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Re: equação exponencial
Re: equação exponencial
ta certo, valeu
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Re: equação exponencial
Re: equação exponencial
pedro, criei o topico, se poder me ajudar, serio muito bom 
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Re: equação exponencial
Re: equação exponencial
Ótima resolução Pedro
Ademir Sott- Jedi

- Mensagens : 270
Data de inscrição : 14/12/2012
Idade : 55
Localização : Pimenta Bueno, RO, Brasil
 Re: equação exponencial
Re: equação exponencial
Obrigado.

PedroCunha- Monitor

- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Verifique se a equação dada é exata (Equação Diferencial)
» Verifique se a equação dada é exata (Equação Diferencial)
» Verifique se a equação dada é exata (Equação Diferencial)
» Verifique se a equação dada é exata (Equação Diferencial)
» Verifique se a equação dada é exata (Equação Diferencial)
» Verifique se a equação dada é exata (Equação Diferencial)
» Verifique se a equação dada é exata (Equação Diferencial)
» Verifique se a equação dada é exata (Equação Diferencial)
» Verifique se a equação dada é exata (Equação Diferencial)
PiR2 :: Questões Especiais :: Olimpíadas :: Matemática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












