Colégio Naval 97
+3
Luck
Medeiros
iaguete
7 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Colégio Naval 97
Colégio Naval 97
Considere o sistema linear S, de incógnitas x e y :
S= a1x+b1y=c1
a2x+b2y=c2
Se os pares ordenados (x,y)=(3,-5) e (x,y)=(2,-3) são soluções de S, então:
a)(-3,7) também é solução de S
b)(3,-7) também é solução de S
c)S só tem as duas soluções apresentadas
d)S só tem mais uma solução além das apresentadas
e)Qualquer par ordenado de números reais é solução de S
gabarito: a
S= a1x+b1y=c1
a2x+b2y=c2
Se os pares ordenados (x,y)=(3,-5) e (x,y)=(2,-3) são soluções de S, então:
a)(-3,7) também é solução de S
b)(3,-7) também é solução de S
c)S só tem as duas soluções apresentadas
d)S só tem mais uma solução além das apresentadas
e)Qualquer par ordenado de números reais é solução de S
gabarito: a
iaguete- Jedi

- Mensagens : 253
Data de inscrição : 13/05/2012
Idade : 30
Localização : rio de janeiro
 Re: Colégio Naval 97
Re: Colégio Naval 97
substituindo os pontos no sistema S:
(3, -5):
{3a1 - 5b1 = c1 ............(i)
{3a2 - 5b2 = c2 ............(ii)
(2, -3)
{2a1 - 3b1 = c1 ............(iii)
{2a2 - 3b2 = c2 ............(iv)
(i)=(ii): ------> a1 = 2b1 -----> c1 = b1 ..........(v)
(iii)-(iv): -----> a2 = 2b2 -----> c2 = b2 ..........(vi)
levando os resustados (v) e (vi) no sistema S:
{ 2b1.x + b1.y = b1
{ 2b2.x + b2.y = b2
dividindo respectivamente por b1 e b2; com b1≠0 e b2≠0 (caso contrário, não existe o sistema com duas variáveis), vem:
{ 2x + y = 1
{ 2x + y = 1
portanto: 2x + y = 1 ................... uma reta
p/ x=3 ---> y=-5
p/ x=2 ---> y=-3 ..........confirma os pontos dados no enunciado.
alternativas:
a) p/ x=-3 ---> y=7 ........ verdade
b) p/ x=3 ---> y=-5 ≠ -7 ........falso
c) falso ....... S, sendo uma reta, tem infinitas soluções.
d) falso (vide item c)
e) falso ....... apenas serão soluções de S os pares ordenados sobre a reta.
(3, -5):
{3a1 - 5b1 = c1 ............(i)
{3a2 - 5b2 = c2 ............(ii)
(2, -3)
{2a1 - 3b1 = c1 ............(iii)
{2a2 - 3b2 = c2 ............(iv)
(i)=(ii): ------> a1 = 2b1 -----> c1 = b1 ..........(v)
(iii)-(iv): -----> a2 = 2b2 -----> c2 = b2 ..........(vi)
levando os resustados (v) e (vi) no sistema S:
{ 2b1.x + b1.y = b1
{ 2b2.x + b2.y = b2
dividindo respectivamente por b1 e b2; com b1≠0 e b2≠0 (caso contrário, não existe o sistema com duas variáveis), vem:
{ 2x + y = 1
{ 2x + y = 1
portanto: 2x + y = 1 ................... uma reta
p/ x=3 ---> y=-5
p/ x=2 ---> y=-3 ..........confirma os pontos dados no enunciado.
alternativas:
a) p/ x=-3 ---> y=7 ........ verdade
b) p/ x=3 ---> y=-5 ≠ -7 ........falso
c) falso ....... S, sendo uma reta, tem infinitas soluções.
d) falso (vide item c)
e) falso ....... apenas serão soluções de S os pares ordenados sobre a reta.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Re: Colégio Naval 97
Re: Colégio Naval 97
3a1 -5b1 = c1 (.2)
2a1 -3b1 = c1 (.3)
6a1 -10b1 = 2c1
6a1 - 9b1 = 3c1
subtraindo vc obtém: b1 =c1 , a1 = 2c1 , então:
2x + y = 1 , (-3,7) satisfaz, letra a).
2a1 -3b1 = c1 (.3)
6a1 -10b1 = 2c1
6a1 - 9b1 = 3c1
subtraindo vc obtém: b1 =c1 , a1 = 2c1 , então:
2x + y = 1 , (-3,7) satisfaz, letra a).

Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
Jorge Marcelo Da Costa gosta desta mensagem
 Re: Colégio Naval 97
Re: Colégio Naval 97
Agora me deu o "estalo" de que essa solução poderia ser muito mais simples. Vê se concorda:
O sistema é do primeiro grau. Logo, sua representação geométrica é uma reta. Usamos os dois pares ordenados (pontos) fornecidos como solução, para achar a eq. dessa reta.
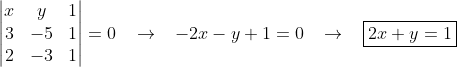
agora é só testar as alternativas.
O sistema é do primeiro grau. Logo, sua representação geométrica é uma reta. Usamos os dois pares ordenados (pontos) fornecidos como solução, para achar a eq. dessa reta.
agora é só testar as alternativas.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Re: Colégio Naval 97
Re: Colégio Naval 97
Medeiros escreveu:Agora me deu o "estalo" de que essa solução poderia ser muito mais simples. Vê se concorda:
O sistema é do primeiro grau. Logo, sua representação geométrica é uma reta. Usamos os dois pares ordenados (pontos) fornecidos como solução, para achar a eq. dessa reta.
agora é só testar as alternativas.
Olá! A representação geométrica de um sistema do primeiro grau não seria um ponto? Fui pesquisar "representação geométrica sistema do primeiro grau" e fiquei com essa dúvida

Suzannie- Iniciante
- Mensagens : 20
Data de inscrição : 03/02/2021
Idade : 19
 Re: Colégio Naval 97
Re: Colégio Naval 97
Suzannie
tudo o que sei é que um sistema em que há duas variáveis (x e y) e é do 1º grau, a única representação que conheço é a reta.
um ponto não forma um sistema; um ponto é apenas uma coordenada. Mas, se tivermos uma sequência de vários pontos, obedecendo uma lei específica, aí este conjunto forma um sistema.
tudo o que sei é que um sistema em que há duas variáveis (x e y) e é do 1º grau, a única representação que conheço é a reta.
um ponto não forma um sistema; um ponto é apenas uma coordenada. Mas, se tivermos uma sequência de vários pontos, obedecendo uma lei específica, aí este conjunto forma um sistema.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Re: Colégio Naval 97
Re: Colégio Naval 97
Suzannie
Por definição, um sistema do 1º grau é sempre do tipo: y = m.x + n, com m ≠ 0
O gráfico é uma reta que corta o eixo y na ordenada n
A reta faz, com o eixo x positivo, um ângulo θ, tal que m = tgθ
Por definição, um sistema do 1º grau é sempre do tipo: y = m.x + n, com m ≠ 0
O gráfico é uma reta que corta o eixo y na ordenada n
A reta faz, com o eixo x positivo, um ângulo θ, tal que m = tgθ

Elcioschin- Grande Mestre

- Mensagens : 73184
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Colégio Naval 97
Re: Colégio Naval 97
alguém poderia me explicar como ele chegou nessa equação através do método dele
equação 2x+y=1
meu pensamento foi que ele trocou o c1= x mas mas nao faria sentido....

Am3nicLordX- Iniciante
- Mensagens : 43
Data de inscrição : 28/02/2022
 Re: Colégio Naval 97
Re: Colégio Naval 97
Am3nicLordX escreveu:
alguém poderia me explicar como ele chegou nessa equação através do método dele
equação 2x+y=1
meu pensamento foi que ele trocou o c1= x mas mas nao faria sentido....
6a1 - 10b1 = 2c1 (I)
-6a1 + 9b1 = -3c1 (II)
________________
---> b1 = c1, daí substituindo isso em (I):
6a1 - 10c1 = 2c1
6a1 = 12c1
.:. a1 = 2c1
Colocando a primeira equação em função de c1:
a1x + b1y = c1 ---> 2c1.x + c1.y = c1, dividindo por c1, temos: 2x + y = 1
Daí eu acho que ele testou as alternativas e encontrou um par ordenado como solução...

castelo_hsi- Mestre Jedi

- Mensagens : 625
Data de inscrição : 27/06/2021
Localização : São Paulo - SP
Am3nicLordX gosta desta mensagem
 Re: Colégio Naval 97
Re: Colégio Naval 97
tava dificil de enxergar vlw @castelo_hsi

Am3nicLordX- Iniciante
- Mensagens : 43
Data de inscrição : 28/02/2022
castelo_hsi gosta desta mensagem
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












