Calculo Operacional
Página 1 de 1
 Calculo Operacional
Calculo Operacional
Alguém pode me explicar como é que o camarada resolveu esta equação?

http://es.wikipedia.org/wiki/Transformada_de_Laplace
http://es.wikipedia.org/wiki/Transformada_de_Laplace
Convidado- Convidado
 Re: Calculo Operacional
Re: Calculo Operacional
Estudando transformada de Laplace ein cara.
Minha preferida. Esta equação trata de uma demostração de como podemos resolver uma equação diferencial substituindo termos operacionais por membros algébricos. É um método interessante geralmente utilizado na introdução a esse tipo de cálculo, já que se fundamenta nos mesmos princípios de todas as formas de transformada para este emprego.
A equação original é:
}{\mathrm{d}&space;x}-\alpha&space;y(x)=f(x))
Chamando o operador derivada de D, transforma-se em:
y=f(x))
Considerando que (D-α) é um operador algébrico( afinal, é nisto que se baseia o cálculo operacional):
}{(D-\alpha)})
Agora vem o passo mais importante. Olhando na equação:
)
Sabemos que:
dx&space;=\frac{f(x)}{D-\alpha})
Assim o operador 1/D é a operação integral. Como era de se esperar já que são operações inversas. Prosseguindo com a equação anterior, a ideia é reduzir 1/(d- α ) em uma série de operações inversas que possam ser convertidas em integrais e a equação será resolvida. Assim tratamos deste denominador como um polinômio e expandimos-o em séries de taylor:
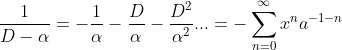
Para isso suponhamos que f(x)=x^2 e a=1:
x^2=-(x^2+2x+1))
Que é a solução de nossa equação que também poderia ser encontrada na forma geral que você indicou. Note que c1 é a constante de integração. Você poderia Testar com várias outras funções e concluir que o método é eficiente para qualquer equação em que o operador possa ser organizado como um polinômio e expandi-lo derivando cada termo da função na ordem encontrada encontrando a função solução.
Você pode provar facilmente que a fórmula geral funciona aplicando D-a ao lado direito encontrando f. Uma demonstração dela nada rigorosa masa que pode ajudar seria da seguinte forma:
Queremos:
}{D-a})
Multiplicando por e^(1-at):
}{D-a})
Mas observe que podemos modificar o lado direito a fim de que tenhamos expoente igual a denominador, lembrando que (D-a)t=1=at:
}{D-a}=e^{(D-a)t}\frac{f(x)}{D-a}=e.e^{-at}\frac{f(x)}{D})
A última passagem, por parecer estranha é plausível pois tratando D como algo puramente algébrico mas considerando suas propriedades:
t}=(D-a)e^{(D-a)t}==>-ae^{(D-a)t}=0)
O que não é completamente justificável. Assim para admitir a última passagem consideremos a natureza operacional de e^(d-a)t e o inverso sob todos os termos do lado, que são meramente algébricos! Assim antes de mais nada:
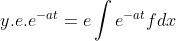
Entretanto into não prova nada além de que é possível representar operações diferenciais como termos algébricos.
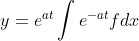
Onde fica D-a ≈ D para as exponenciais
Para algo completo sugiro que continue seus estudos com transformada de Laplace onde encontrará a relação:
Minha preferida. Esta equação trata de uma demostração de como podemos resolver uma equação diferencial substituindo termos operacionais por membros algébricos. É um método interessante geralmente utilizado na introdução a esse tipo de cálculo, já que se fundamenta nos mesmos princípios de todas as formas de transformada para este emprego.
A equação original é:
Chamando o operador derivada de D, transforma-se em:
Considerando que (D-α) é um operador algébrico( afinal, é nisto que se baseia o cálculo operacional):
Agora vem o passo mais importante. Olhando na equação:
Sabemos que:
Assim o operador 1/D é a operação integral. Como era de se esperar já que são operações inversas. Prosseguindo com a equação anterior, a ideia é reduzir 1/(d- α ) em uma série de operações inversas que possam ser convertidas em integrais e a equação será resolvida. Assim tratamos deste denominador como um polinômio e expandimos-o em séries de taylor:
Para isso suponhamos que f(x)=x^2 e a=1:
Que é a solução de nossa equação que também poderia ser encontrada na forma geral que você indicou. Note que c1 é a constante de integração. Você poderia Testar com várias outras funções e concluir que o método é eficiente para qualquer equação em que o operador possa ser organizado como um polinômio e expandi-lo derivando cada termo da função na ordem encontrada encontrando a função solução.
Você pode provar facilmente que a fórmula geral funciona aplicando D-a ao lado direito encontrando f. Uma demonstração dela nada rigorosa masa que pode ajudar seria da seguinte forma:
Queremos:
Multiplicando por e^(1-at):
Mas observe que podemos modificar o lado direito a fim de que tenhamos expoente igual a denominador, lembrando que (D-a)t=1=at:
A última passagem, por parecer estranha é plausível pois tratando D como algo puramente algébrico mas considerando suas propriedades:
O que não é completamente justificável. Assim para admitir a última passagem consideremos a natureza operacional de e^(d-a)t e o inverso sob todos os termos do lado, que são meramente algébricos! Assim antes de mais nada:
Entretanto into não prova nada além de que é possível representar operações diferenciais como termos algébricos.
Onde fica D-a ≈ D para as exponenciais
Para algo completo sugiro que continue seus estudos com transformada de Laplace onde encontrará a relação:

Matheus Fillipe- Mestre Jedi

- Mensagens : 893
Data de inscrição : 19/05/2013
Idade : 27
Localização : Araxá
 Tópicos semelhantes
Tópicos semelhantes» Amplificador Operacional
» Amplificador Operacional
» Ganho Amplificador Operacional
» LaTeX operacional novamente
» Sistema operacional posicional
» Amplificador Operacional
» Ganho Amplificador Operacional
» LaTeX operacional novamente
» Sistema operacional posicional
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












