números complexos e geometria

por **mauk03** Seg 20 maio 2013, 13:00

Considerem-se, no plano de Argand-Gauss, os subconjuntos $A=\left \{ z\in \mathbb{C}\mid Re\left ( \frac{1}{z} \right )\geq \frac{1}{4} \right \}$ e $B=\left \{ z\in \mathbb{C}\mid Im\left ( z \right )\leq \sqrt{3}\right \}$ . Calcule a área da região definida por $A\cap B$ .

por Luck Seg 20 maio 2013, 15:43

z = x + yi
1/z = 1/(x+yi) = (x - yi) / (x²+y²)
Re(1/z) ≥ 1/4
x/(x²+y²) ≥ 1/4 ∴ (x²+y²)/x ≤ 4 ∴ (x² + y² -4x) /x ≤ 0
se x < 0 , x² + y² -4x ≥ 0 ,o que é verdade sempre.
se x > 0 , x² + y²-4x ≤ 0, (x-2)² + y² ≤ 2² , o que representa o interior de uma circunferência C(2,0) e R = 2 ,

Im(z) ≤ √3
y ≤ √3
entao a área A que procuramos é a área da circuferência subtraído da parte azul.
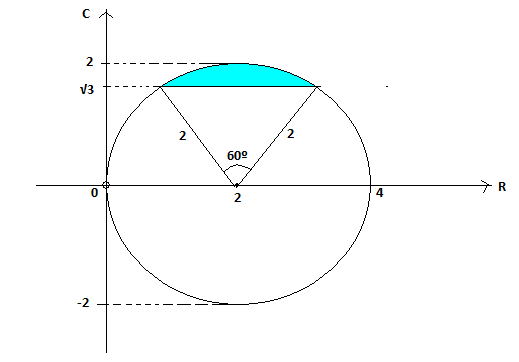
números complexos e geometria Untitled2