Sistema
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Sistema
por Feehs Qua 20 Fev 2013, 13:37
(IME - 71) Resolva o sistema :
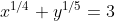
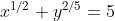
R : x = 1 ; y = 32
x = 16 ; y = 1
R : x = 1 ; y = 32
x = 16 ; y = 1
Feehs- Recebeu o sabre de luz
- Mensagens : 103
Data de inscrição : 26/01/2012
Idade : 31
Localização : SP/SP/Brasil
Re: Sistema
por Luck Qua 20 Fev 2013, 14:03
x^(1/4) = t
x^(1/2) = t²
y^1/5 = k
y^(2/5) = k²
t + k = 3
t² + k² = 5 --> (t+k)² - 2tk = 5 --> 2tk = 4 -> tk = 2
seja a equação: w² - 3w + 2 = 0 , onde as raízes sao t e k
t = 1 ou k = 2
x^(1/4) = 1 --> x = 1
y^(1/5) = 2 --> y = 32
ou t = 2 , k = 1
x^(1/4) = 2 --> x = 16
y^(1/5) =1 --> y = 1
S = { (1 , 32) ; (16 , 1) }
x^(1/2) = t²
y^1/5 = k
y^(2/5) = k²
t + k = 3
t² + k² = 5 --> (t+k)² - 2tk = 5 --> 2tk = 4 -> tk = 2
seja a equação: w² - 3w + 2 = 0 , onde as raízes sao t e k
t = 1 ou k = 2
x^(1/4) = 1 --> x = 1
y^(1/5) = 2 --> y = 32
ou t = 2 , k = 1
x^(1/4) = 2 --> x = 16
y^(1/5) =1 --> y = 1
S = { (1 , 32) ; (16 , 1) }
Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
