polígono regular

por jessicajessica Seg Nov 19 2012, 17:57

Calcular a área do seguinte polígono regular:
-Um octógono, de apótema 8 cm.

resposta: 512( √2-1)

por **Matheus Vilaça** Seg Nov 19 2012, 19:55

Temos o seguinte caso: Onde A=Apótema/R=raio/L=Lado

[img]

[/img]

Matematicamente temos que
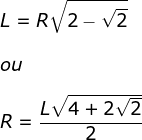
$\fn_jvn \\L=R\sqrt{2-\sqrt{2}}\\ \\ou\\ \\R=\frac{L\sqrt{4+2\sqrt{2}}}{2}$

Do triângulo em destaque temos que:
$\small \fn_jvn (\frac{L\sqrt{4+2\sqrt{2}}}{2})^2=64+\frac{L^2}{4}$

Logo, da equação descobrimos que:
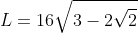
$L=16\sqrt{3-2\sqrt{2}}$

Eu não sei se você viu isso, mas é possível simplificar o caso acima da seguinte forma:

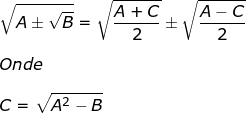
$\small \fn_jvn \\\sqrt{A\pm \sqrt{B}}=\sqrt{\frac{A+C}{2}}\pm \sqrt{\frac{A-C}{2}}\\ \\Onde\\ \\C=\sqrt{A^2-B}$

Fazendo isso, você verá que:
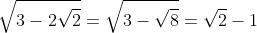
$\sqrt{3-2\sqrt{2}}=\sqrt{3-\sqrt{8}}=\sqrt{2}-1$

Logo:
${\color{Red} L=16(\sqrt{2}-1)}$

Assim a área de um dos triângulos do octógono será:
$A=\frac{16(\sqrt{2}-1).8}{2}=64(\sqrt{2}-1)$

Como são oito triângulos que formam o octógono:
$At=8.64(\sqrt{2}-1)={\color{Red} 512(\sqrt{2}-1)}$

É isso. Boa questão!!!!! Smile

por **Matheus Vilaça** Ter Nov 20 2012, 14:34

Caso queira saber a dedução da simplificação das raízes que eu mostrei acima, vou postar aqui!!!!!!

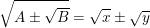
$\small \dpi{100} \\\sqrt{A\pm \sqrt{B}}=\sqrt{x}\pm \sqrt{y}\\$

Elevando ambos ao quadrado:
$\small \dpi{100} \\(\sqrt{A\pm \sqrt{B}})^2=(\sqrt{x}\pm \sqrt{y})^2\\ \\A\pm \sqrt{B}=x+y\pm 2\sqrt{xy}$

Dessa última obtemos o sistema:
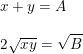
$\small \dpi{100} \\x+y=A\\ \\2\sqrt{xy}=\sqrt{B}$

Que é equivalente a:
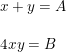
$\small \dpi{100} \\x+y=A\\ \\4xy=B$

Do sistema obtemos a seguinte equação do segundo grau:
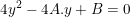
$\small \dpi{100} 4y^2-4A.y +B=0$

Logo, por Bháskara:
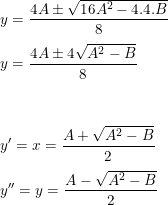
$\small \dpi{100} \\y=\frac{4A\pm \sqrt{16A^2-4.4.B}}{8}\\ \\y=\frac{4A\pm 4\sqrt{A^2-B}}{8}\\ \\\\\\y'=x=\frac{A+\sqrt{A^2-B}}{2}\\ \\y''=y=\frac{A-\sqrt{A^2-B}}{2}\\$

Estabelecendo que:
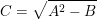
$\small \dpi{100} C=\sqrt{A^2-B}$

Assim, obtemos:
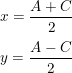
$\small \dpi{100} \\x=\frac{A+C}{2}\\ \\y=\frac{A-C}{2}\\$

Logo, da primeira equação escrita, obtemos que:
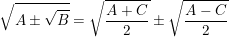
$\small \dpi{100} \sqrt{A\pm \sqrt{B}}=\sqrt{\frac{A+C}{2}}\pm \sqrt{\frac{A-C}{2}}$

Onde esse sinal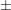 $\small \dpi{100} \pm$ indica que o sinal a ser colocado depende do sinal da "dupla raíz". Se for negativo ali, também será negativo do outro "lado". Se for positivo ali, também será positivo do outro "lado".

----------------------------------------------------------------------------------------------------------------------

Para a relação entre o raio e o lado do octógono, temos o seguinte caso:
[img]

[/img]

Como o octógono é formado por 8 triângulos iguais, o ângulo a da figura será:
$\small \dpi{100} a=\frac{360º}{8}=45º$

Utilizando lei dos cossenos no triângulo:
$\small \dpi{100} \\L^2=R^2+R^2-2.R.R.cos45º\\ \\L^2=2R^2-2R^2.\frac{\sqrt{2}}{2}\\ \\\\L^2=2R^2-\sqrt{2}R^2\\ \\L^2=R^2(2-\sqrt{2})\\\\ {\color{Red} \\\\L=R\sqrt{2-\sqrt{2}}}$

Eu não sei se era necessário, mas com a dedução sempre fica mais claro caso você queira saber!!!!! Smile

por jessicajessica Ter Nov 20 2012, 21:08

Obg gente

por **Medeiros** Qua Nov 21 2012, 03:23

É de muito bom nível a resposta do participante Matheus.
Apresento um segundo modo bem simples.

Se o octógono é regular, então é inscritível num quadrado. Seja L o lado do octógono.

se o apótema a=8 -----> lado do quadrado = 2a

x√2 = L -----> x = L/√2 = L√2/2

2a = L + 2x -----> 2a = L + L√2 -----> L = 2a/(1+√2) -----> L = 2a(√2-1) cm

Area do octógono (A) será oito vezes a área do triângulo assinalado.

A = 8*(L*a/2) -----> A = 4*2a²(√2 - 1) -----> A = 8(√2 - 1)a² -----> A = 512(√2 - 1) cm²

por Conteúdo patrocinado

polígono regular

polígono regular

Re: polígono regular

Re: polígono regular

Re: polígono regular

Re: polígono regular

Re: polígono regular

Um fórum livre e democrático.