Polígono Regular

por JpGonçalves_2020 Dom 11 Dez 2022, 22:20

Se A, B, C e D são quatro vértices consecutivos de um polígono regular, temos que [latex]\frac{1}{AB} = \frac{1}{AC} + \frac{1}{AD} [/latex]. Quantos lados o polígono tem?

por **Elcioschin** Seg 12 Dez 2022, 13:15

Tens o gabarito? Eu acho que a resposta é 7 ---> heptágono regular

Uma questão similar caiu no vestibular de engenharia de 1965 da UFJF (Juiz de Fora - MG), no qual eu fui aprovado.
Ela foi proposta pelo famoso professor Morgado do IMPA do RJ, o qual foi meu professir de GA na faculadade. Ele pode ser resolvida usando o Teoreme de Hiparco (ou Ptolomeu)
Eu postei esta questão fórum há algum tempo atrás e está resolvida. Pesquise!
O enunciado é mais ou menos este "Prove que, num heptágono regular ABCDEFGA, 1/AB = 1/AC + 1/AD"

por **petras** Seg 12 Dez 2022, 13:50

Élcio , na questão da época já era informado que era um heptágono. Como deduzir apenas em função da relação que seria um heptágono?
https://pir2.forumeiros.com/t4798-ufjf-1965-heptagono-regular

por **petras** Ter 13 Dez 2022, 10:15

Elcioschin escreveu:Tens o gabarito? Eu acho que a resposta é 7 ---> heptágono regular

Uma questão similar caiu no vestibular de engenharia de 1965 da UFJF (Juiz de Fora - MG), no qual eu fui aprovado.
Ela foi proposta pelo famoso professor Morgado do IMPA do RJ, o qual foi meu professir de GA na faculadade. Ele pode ser resolvida usando o Teoreme de Hiparco (ou Ptolomeu)
Eu postei esta questão fórum há algum tempo atrás e está resolvida. Pesquise!
O enunciado é mais ou menos este "Prove que, num heptágono regular ABCDEFGA, 1/AB = 1/AC + 1/AD"

Segue uma solução por trigonometria.

Sendo x a metade do ângulo central:

[latex]AB=2rsen(x)\\ AC=2rsen(2x)\\ AD=2rsen(3x)\\ \therefore \frac{1}{sen(x)}=\frac{1}{sen2x}+\frac{1}{sen3x}\implies \frac{1}{sen(x)}-\frac{1}{sen2x}=\frac{1}{sen3x}\\ \\sen(2x)=2sen(x)cos(x):\frac{2cos(x)-1}{sen(2x)}=\frac{1}{sen(3x)}\\ \therefore 2sen(3x)cos(x)-sen(3x)=sen(2x)\\ sen(A)cos(B)=\frac{{}sen(A+B)+sen(A-B)}{2}:\\ sen(4x)+sen(2x)-sen(3x)=sen(2x) \implies sen(4x)=sen(3x)\\ \cancel{x=0}\therefore 4x+3x=180^o. \implies \boxed{x=\frac{180^o}{7}}.[/latex]

(Solução:LuizFuentes)

por **Elcioschin** Ter 13 Dez 2022, 11:23

Excelente petras!
Quanto à presente questão eu nem pensei em procurar um caminho, já que, para mim, a solução era óbvia.
É fácil provar que a solução não vale para um quadrado, para um pentágono regular, nem para um hexágono.
A solução vale para um heptágono regular, mas não signifca que não valha para um poligono regular de mais de 7 lados.
Então a solução continua pendente. Quem sabe algum outro colega do fórum consegue provar!

por **petras** Qui 15 Dez 2022, 10:04

Elcioschin escreveu:Excelente petras!
Quanto à presente questão eu nem pensei em procurar um caminho, já que, para mim, a solução era óbvia.
É fácil provar que a solução não vale para um quadrado, para um pentágono regular, nem para um hexágono.
A solução vale para um heptágono regular, mas não signifca que não valha para um poligono regular de mais de 7 lados.
Então a solução continua pendente. Quem sabe algum outro colega do fórum consegue provar!

Segue uma solução por geometria:

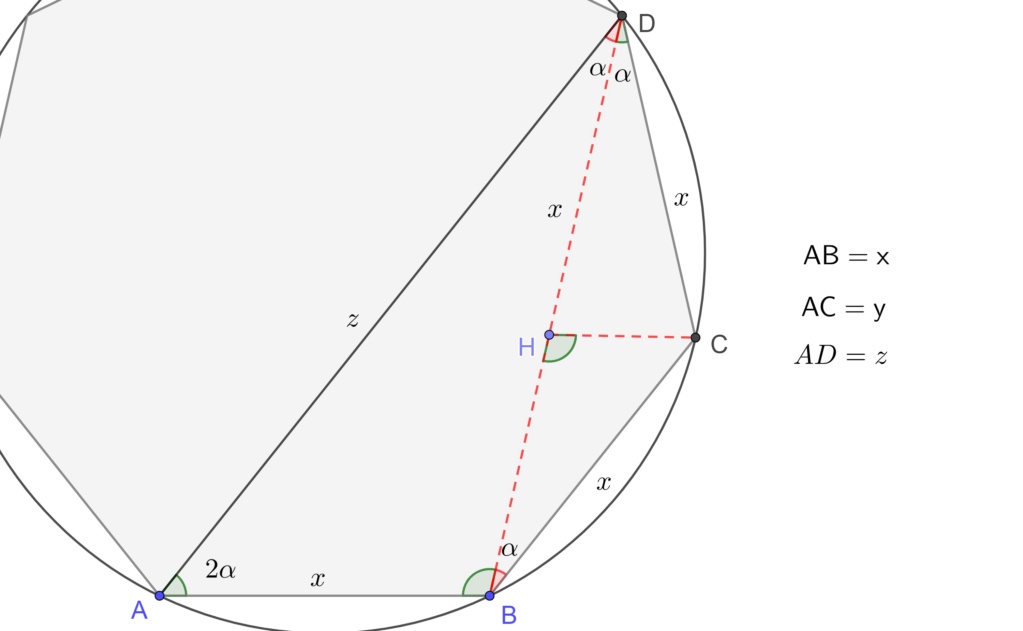
[latex]AB=x:AC=y :AD=z.\\ H \in BD (DH=x) \implies \angle DHC=\frac{180^o-\alpha}{2}=\frac{90^o-\alpha}{2}\\ \angle BHC=180^o-(\frac{90^o-\alpha}{2})=\frac{90^o+\alpha}{2}(1)\\ \angle ABD=180^o-3\alpha(2)\\ BD=AC\implies HB=y-x(3)\\ \frac{1}{AB}=\frac{1}{AC}+\frac{1}{AD} \implies\frac{1}{x}=\frac{1}{y}+\frac{1}{z}\\ \therefore \frac{y-x}{x}=\frac{y}{z} \implies \frac{HB}{BC}=\frac{BD}{DA}\\ \therefore \angle BDA=\angle HBC=\alpha\\ \therefore \triangle DBA \sim \triangle BHC \implies \angle DBA=\angle BHC(4)\\ (1)e(2)em(4): 180^o-3\alpha=90^o+\frac{\alpha}{2}\\ \boxed{\alpha=\frac{180^o}{7}}[/latex]
(Solução:LiKwok)