Geometria Plana

por Bia102007 Qua 23 maio 2012, 18:08

No retângulo PQRS as medidas dos lados PQ e PS são, respectivamente, 15 m e 10 m. Pelo ponto médio, F, do lado PS traça-se o segmento FR dividindo o retângulo em duas partes. Se E é o ponto do lado PQ tal que a medida do segmento EQ é 5 m, traça-se por E uma perpendicular a FR determinando o ponto G em FR. Nestas condições, a medida da área, em metros quadrados, do quadrilátero PFGE é:

A) 50,25

B) 53,25

C) 56,25 <-- Por quê?

D) 59,25

por pcpcoast Qua 23 maio 2012, 20:36

Da maneira que eu fiz deu uma página e meia do meu caderno (até porque eu desenhei um pouco né... )

Mas tipo, eu fiz por analítica. Então, se ninguém postar a resposta aqui, postarei a minha depois.

PS.: Sacas de Geometria Analítica?

por pcpcoast Qui 24 maio 2012, 21:48

Fiz por plana, só deu um pouco mais de conta, mas segue aí:

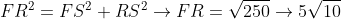
$Geometria Plana Gif$

$Geometria Plana Gif$

Vemos que os triângulos: PEF e EQR são semelhantes, logo, FG = GR = FR/2.
Vamos então, descobrir a medida do segmento EG utilizando pitágoras:

FE² = FG² + EG²

$Geometria Plana Gif$

Vemos, então, que o triângulo EFG é isósceles.

Agora, para calcular a área...

Área de EFP + área de EFG =

$Geometria Plana Gif.latex?\frac{10.5}{2} + (\frac{5\sqrt{10}}{2})^{2}$

por **Medeiros** Sáb 26 maio 2012, 04:14

bem resolvido Pcpcoast.

por IsaacR2 Sáb 01 Jul 2017, 17:10

pcpcoast escreveu:Fiz por plana, só deu um pouco mais de conta, mas segue aí:

$Geometria Plana Gif$

$Geometria Plana Gif$

Vemos que os triângulos: PEF e EQR são semelhantes, logo, FG = GR = FR/2.
Vamos então, descobrir a medida do segmento EG utilizando pitágoras:

FE² = FG² + EG²

$Geometria Plana Gif$

Vemos, então, que o triângulo EFG é isósceles.

Agora, para calcular a área...

Área de EFP + área de EFG =

$Geometria Plana Gif.latex?\frac{10.5}{2} + (\frac{5\sqrt{10}}{2})^{2}$

Como eu sei que PEF e EQR são semelhantes? Não consegui ver nenhum método de semelhança confused

por **Medeiros** Sáb 01 Jul 2017, 17:35

PEF e EQR são dois triângulos retângulos (pois têm os ângulos do retângulo) com os catetos de mesma medida, 5 m e 10 m. Na verdade, são triângulos congruentes, caso LAL.

Na realidade,existe um modo ainda mais fácil de obter a resposta:
A = (1/2).(3/4).(área do retângulo) = (1/2).(3/4).15*10 = 56,25
Mas isto depende de perceber que os quadriláteros PEGF e EQRG têm mesma área. O que depende de perceber, além da congruência dos triângulos acima citados, também que são congruentes os triângulos FGE e RGE. Então a área desejada é metade da do quadrilátero PQRF, que por sua vez vale 3/4 da do retângulo.