Área do Triângulo

por Aline Qui 5 Abr 2012 - 12:24

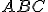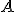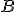Considera-se um triângulo $Área do Triângulo Mimetex$ , com área igual à $Área do Triângulo Mimetex$ . Traça-se uma reta $Área do Triângulo Mimetex$ passando pelos vértices $Área do Triângulo Mimetex$ e $Área do Triângulo Mimetex$ . Traça-se uma outra reta $Área do Triângulo Mimetex$ paralela a esta, porém passando pelo vértice $Área do Triângulo Mimetex$ . Distante $Área do Triângulo Mimetex$ do vértice $Área do Triângulo Mimetex$ , marca-se um ponto $Área do Triângulo Mimetex$ . Liga-se os pontos $Área do Triângulo Mimetex$ , formando um novo triângulo. A área do triângulo $Área do Triângulo Mimetex$ é igual a:

a) $Área do Triângulo Mimetex.cgi?250\tex{ cm^2}$
b) $Área do Triângulo Mimetex.cgi?55\tex{ cm^2}$
c) $Área do Triângulo Mimetex.cgi?27,5\tex{ cm^2}$
d) $Área do Triângulo Mimetex.cgi?110\tex{ cm^2}$
e) $Área do Triângulo Mimetex.cgi?50\tex{ cm^2}$

por **Medeiros** Qui 5 Abr 2012 - 18:55

faça um desenho para enxergar melhor.
A base do ∆ABC é o segmento AB.
A altura do ∆ABC é a distância entre as retas r e s.
Ora, o ∆ABP tem mesma base e mesma altura do ∆ABC, logo tem a mesma área.
S_∆ABP = 50 cm² ........... (e)

obs.: qualquer ponto X que se coloque sobre a reta s resultará num triângulo ABX de mesma área do triâng. ABC.

Área do Triângulo

Área do Triângulo

Re: Área do Triângulo

Um fórum livre e democrático.