Definição de operação
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Definição de operação
Definição de operação
5. Considere o conjunto dos números inteiros, Z, e defina a seguinte operação:
∗ : Z × Z → Z
(x, y) → x ∗ y = 3x + 2y + 1.
Sobre o conjunto A = {x ∈ Z; x ∗ 2 = 2 ∗ x}, assinale a alternativa verdadeira:
(a) 3 ∈ A
(b) A = ∅
(c) A ´e um conjunto infinito
(d) A ´e um conjunto unitário
(e) A ´e um conjunto finito e a soma dos seus elementos é um número ímpar.
gabarito: letra D
∗ : Z × Z → Z
(x, y) → x ∗ y = 3x + 2y + 1.
Sobre o conjunto A = {x ∈ Z; x ∗ 2 = 2 ∗ x}, assinale a alternativa verdadeira:
(a) 3 ∈ A
(b) A = ∅
(c) A ´e um conjunto infinito
(d) A ´e um conjunto unitário
(e) A ´e um conjunto finito e a soma dos seus elementos é um número ímpar.
gabarito: letra D
vambertxs- Iniciante
- Mensagens : 45
Data de inscrição : 29/03/2024
 Re: Definição de operação
Re: Definição de operação
Oi.
Vamos por item. Primeiro. A operação é definida conforme o enunciado diz.
O conjunto A é o conjunto de todos os naturais que comutam com 2 na operação definida.

A b afirma que A é vazio. Trivialmente, 2 comuta com si mesmo, então 2 pertence a A. Mas, por via das dúvidas.
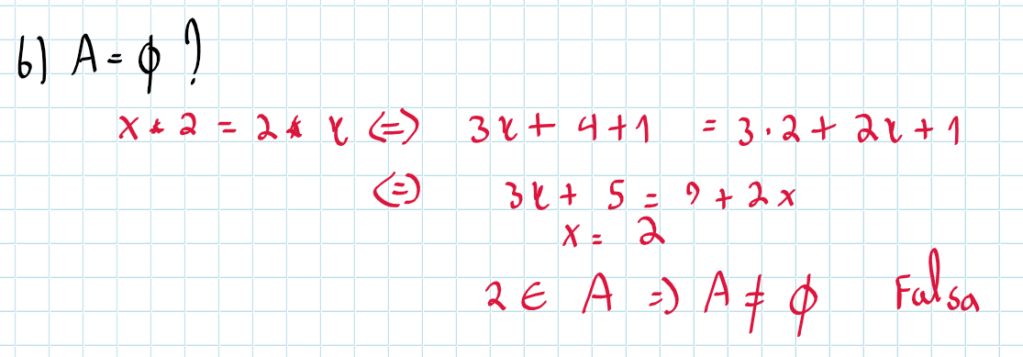
os demais itens já foram respondidos pela b, concorda?
Vamos por item. Primeiro. A operação é definida conforme o enunciado diz.
O conjunto A é o conjunto de todos os naturais que comutam com 2 na operação definida.

A b afirma que A é vazio. Trivialmente, 2 comuta com si mesmo, então 2 pertence a A. Mas, por via das dúvidas.
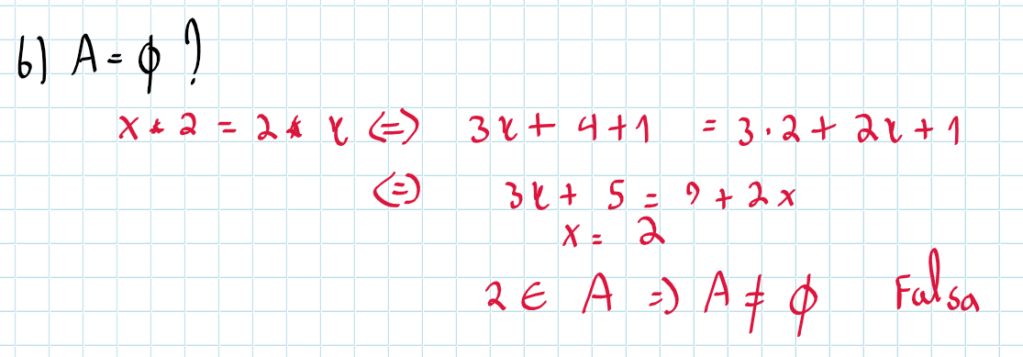
os demais itens já foram respondidos pela b, concorda?
____________________________________________
El Álgebra no es más que Geometría y la Geometría no es más que Álgebra abstracta
Sophie Germain
Sophie Germain
Emanuel Dias- Monitor

- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» (UFF) Operação com log
» operação binaria
» Operação com radicais
» Operação binaria
» Tábuas da operação
» operação binaria
» Operação com radicais
» Operação binaria
» Tábuas da operação
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












