(ITA) Movimento Harmônico Simples

por phBorges_32 Ter 11 Jun 2024, 14:15

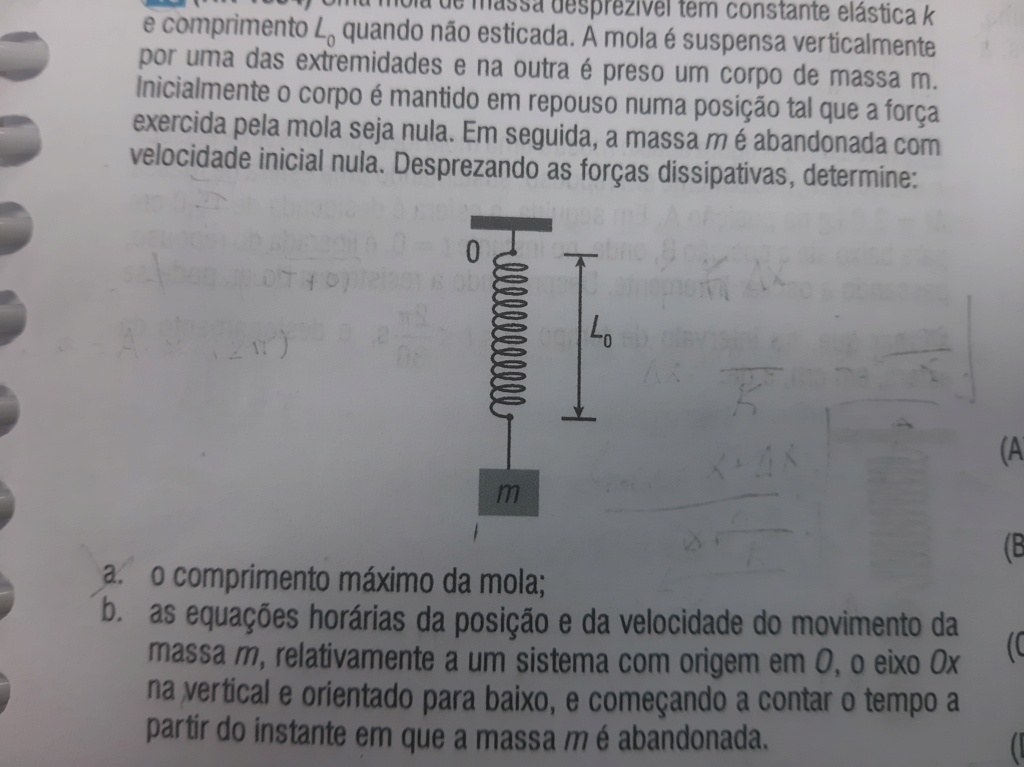
Uma mola de massa desprezível tem constamte elástica k e comprimento Lo, quando não eticada. A mola é supensa verticalmente por uma das extremidades e na outra é preso um corpo de massa m. Inicialmente o corpo é mantido em repouso numa posiçao tal que a força exercida pela mola seja nula. Em seguida, a massa m é abandonada com velocidade icial nula. Desprezando as forças dissipativas, determine:

a. o comprimento máximo da mola;

b. as equações horárias da posição e da velocidade do movimento da massa m, relativamente a um sistema com origem O, o eixo Ox na vertical e orientado para baixo, e começando a contar o tempo a partir do instante em que a massa m é abandonada.

Redpostas:
a. 2mg/k

b. x(t)= Lo + mg/k +mg/k . cos(raiz de(k/m).t + pi)

v(t)= -g. raiz de(m/k). cos(raiz de(k/m).t + pi)

por **Giovana Martins** Ter 11 Jun 2024, 17:47

Inicialmente o sistema está parado na posição 1. Ao ser solto o bloco desce até a posição 2, o que gera a distensão da mola.

Da posição 0 (indicado na figura) até a posição máxima eu vou chamar de ℓ_máx. Inicialmente, portanto, o bloco encontra-se a uma altura corresponde a ℓ_máx - L₀ em relação à posição 2.

Da conservação da energia mecânica, toda a energia potencial gravitacional armazenada na posição 1 será convertida em energia elástica na posição 2, posição na qual a distensão da mola é máxima. Assim, para o item A:

\[\mathrm{E_{m,1}=E_{m,2}\to mg(\ell _{m\acute{a}x}-L_0)=\frac{1}{2}k(\ell _{m\acute{a}x}-L_0)^2\ \therefore\ \boxed{\mathrm{\ell _{m\acute{a}x}=L_0+\frac{2mg}{k}}}}\]

Dado que o sistema é conservativo, após o bloco ser solto, estabelecer-se-á um M.H.S. tal que a amplitude do M.H.S. é dada por:

\[\mathrm{A=\frac{\ell _{m\acute{a}x}-L_0}{2}}\]

0 ___________

|

1

|

1.1

|

2

Veja: de 0 até 1 o comprimento é L₀.

De 1 até 1.1 e 1.1 até 2. o comprimento é A.

A equação da posição do M.H.S., portanto, é dada por:

\[\mathrm{x(t)=L_0+A+Acos(\pi +\omega t), com\ \omega =\sqrt{\frac{k}{m}}\ tal\ que:}\]

\[\mathrm{x(t)=L_0+\frac{\ell _{m\acute{a}x}-L_0}{2}+\left ( \frac{\ell _{m\acute{a}x}-L_0}{2} \right )cos(\pi +\omega t)}\]

\[\mathrm{x(t)=L_0+\frac{mg}{k}+\left (\frac{mg}{k} \right )cos\left ( \pi +t\sqrt{\frac{k}{m}} \right )=L_0+\frac{mg}{k}-\left ( \frac{mg}{k} \right )cos\left ( t\sqrt{\frac{k}{m}} \right )}\]

\[\mathrm{v(t)=\frac{dx(t)}{dt}=\frac{d}{dt}\left [ L_0+\frac{mg}{k}-\left ( \frac{mg}{k} \right )cos\left ( t\sqrt{\frac{k}{m}} \right ) \right ]}\]

\[\mathrm{v(t)=g\sqrt{\frac{m}{k}}sin\left (t\sqrt{\frac{k}{m}} \right ) }\]

por **Giovana Martins** Ter 11 Jun 2024, 17:48

Peço que confira as continhas, porque eu fiz no "olhômetro". Se notar algum equívoco de continha, me avise.

Atualização 12/06/24 às 08 h 03 min: revisei os cálculos e, ao meu ver, o gabarito referente ao comprimento máximo e à velocidade estão incorretos.

por Matheus0110 Ter 23 Jul 2024, 15:15

Eu cheguei em um resultado diferente, poderia me ajudar a entender no que errei?

a)

A posição em que a mola não exerce força será aquela em que ela não está distendida. Como na situação de equilíbrio ela já está distendida de x', a posição de relaxamento será em L₀- x'. Sendo assim, na posição L₀- x' o bloco começará a oscilar em MHS, com a posição de equilíbrio sendo L₀, e, por isso, a posição de maior extensão da mola se dará em L₀ + x'.

Para encontrar x', basta fazer F_el= P, na posição de equilíbrio. Assim:

x' = mg/k

Desta maneira o comprimento máximo será d_máx= L₀ + mg/k

b)

Porque considerei a posição de equilíbrio em L₀, minhas equações de posição e velocidade se modificaram conforme o esperado, ou seja:

[latex]x=L_0+\left ( \frac{mg}{k} \right)cos\left ( \sqrt{\frac{k}{m}}+\pi \right )[/latex]

[latex]v=-g\sqrt{\frac{m}{k}}sen\left ( \sqrt{\frac{k}{m}}+\pi \right )[/latex]

Perceba que a fórmula da velocidade continua a mesma, pois não depende de onde for considerado a posição de equilíbrio.