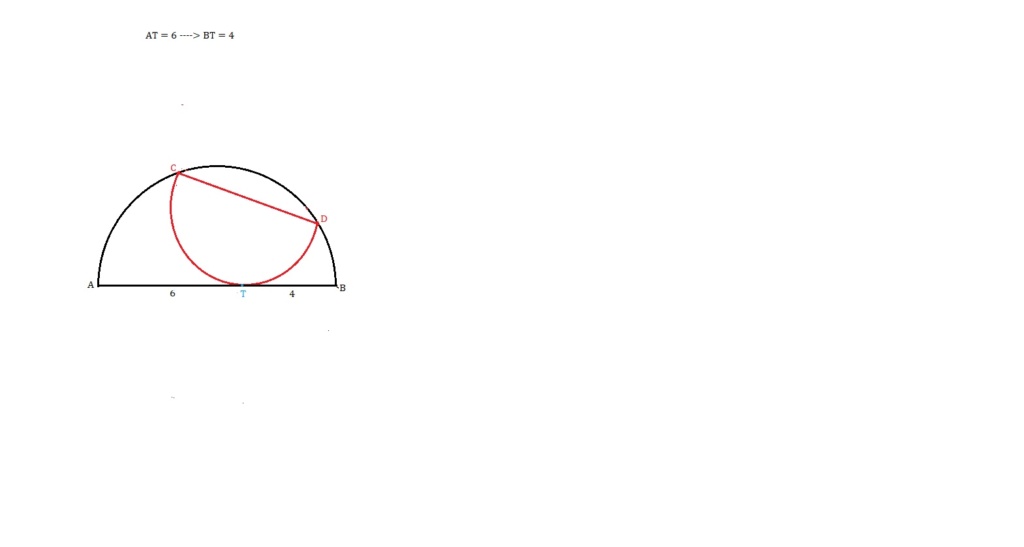
Os dois semicírculos

por **Elcioschin** Ter 19 Mar 2024, 17:52

Temos na figura dois semicírculos, um preto e um vermelho. Ambos se tangenciam em T. Qual é a área do semicírculo vermelho?

por **Medeiros** Qua 20 Mar 2024, 01:13

Tem gabarito?

Na minha conta dá 24.π mas só terei tempo de fazer explicadinho no fim de semana. Agora estou no celular.

Nem precisaria avisar mas só por desencargo de consciência: se alguém quiser responder, fique à vontade (aqui ninguém guarda lugar).

por **Elcioschin** Qua 20 Mar 2024, 08:48

Acho que o gabarito é 6.pi

Vamos deixar o pessoal "queimar as pestanas"!

por **petras** Qua 20 Mar 2024, 09:27

Segue uma solução.

Unindo os dois centros e prolongando até a semicircunferência maior teremos o Raio(R) que divide o diâmetro(FG) ao meio, portanto teremos esse raio perpendicular ao diâmetro.

[latex]\\R=\frac{10}{2}=5\\ CD = FG = DG=r\\ \triangle DFG:R^2 = OD^2+r^2 \implies OD^2=25-r^2\\ \triangle ODC: OD^2 = OC^2+r^2 \implies OD^2 = 1+r^2\\ \therefore 25-r^2 = 1-r^2 \implies r^2 = 12\\ \S = \frac{\pi r^2}{2} = \boxed{6\pi} [/latex]