Ondas em recipientes

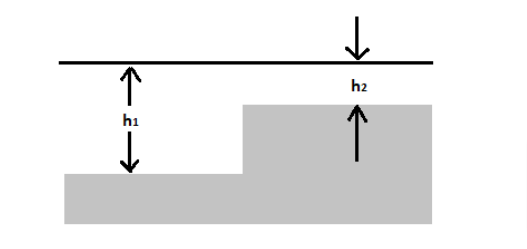
Na figura abaixo, está representada a secção transversal de um recipiente infinitamente grande com um líquido. Da esquerda, do meio que tem uma profundidade \(h_1\), e sob um ângulo de \(\Phi_1\) , em relação ao limite de divisão, movimenta-se uma onda plana, cujo comprimento é \(\lambda >> h_1\) . Que ângulo com o limite de divisão formará essa onda no meio, cuja profundidade do líquido é \(h_2\)?
Sabe-se que a velocidade de propagação das ondas gravitacionais longas, em um recipiente infinitamente grande, é igual a \(v = k\sqrt{hr}\), onde k é o coeficiente de proporcionalidade e h é a profundidade do recipiente.



Gab: \(sen \Phi _2 = \sqrt{\frac{h_2}{h_1}} sen \Phi _1\)

Quando alguma onda passa de um meio mais profundo para um mais raso (ou vice-versa), sua velocidade é afetada, essa verificação é dada experimentalmente. Sendo assim, a onda, ao atingir a região da direita, se refrata e segue a Lei de Snell:

[latex]\frac{\sin \varphi _{1}}{\sin \varphi _{2}}= \frac{v_{1}}{v_{2}}[/latex]

Substituindo os valores de V de acordo com a fórmula dada, notando que k e r são constantes, e manipulando a equação, chegamos à solução:

[latex]\sin \varphi _{2}=\sqrt{\frac{h_{2}}{h_{1}}}\sin \varphi _{1}[/latex]

Compreendi a resolução, mas estou perdido quanto aos ângulos. Quem seriam eles na figura? Poderia me mostrar?

Claro! Eu considerei que esse ângulo formado é aquele entre a frente de onda e o limite de divisão. Vou pegar um desenho da internet para demonstrar o que digo, pois não consigo fazer um desenho muito bom.


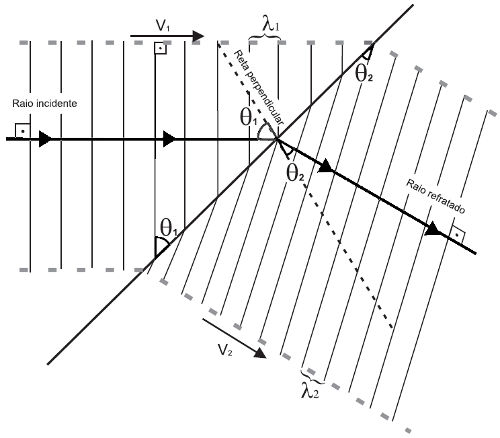
Como pode ver, o ângulo formado entre a frente de onda e o plano de divisão é de "teta". Para o caso de nosso exercício, bastaria rotacionar toda imagem de modo que o plano de divisão fique direcionado "para cima".

Pelo fato de a frente de onda formar um ângulo de 90° com o raio incidente, o ângulo entre o raio incidente e a normal vale também "teta" (perceba que o ângulo complementar de "teta" é também o ângulo complementar entre aquele que fica entre a normal e o raio incidente, e, consequentemente, eles são iguais). A partir daqui é possível prosseguir com a resolução normalmente.

Caso você não tenha entendido muito bem com essa imagem é só me avisar que eu tento desenhar uma representação no caderno.

Agora entendi. Ficou bem mais claro. Muito obrigado pela ajuda!