ESC NAVAL 2022- Volume tetraedro inserido num cubo

por rogermarinha Sáb 14 maio 2022, 20:35

(ESCOLA NAVAL 2022) - Seja o cubo ABCDEFGH de aresta 2 cm e 1, J e K pontos médios das arestas EH, DH e AB, respectivamente.

O volume da pirâmide GIJK, em cm3, é igual a:

A)7/6 ->Gabarito
B)3/2
C)5/4
D)11/8
E)13/12

ESC NAVAL 2022- Volume tetraedro inserido num cubo Cubo10

Gostaria de ratificar este gabarito, alguém se habilita ?

por **petras** Sáb 21 maio 2022, 10:14

A saida mais tranquila é por vetores utilizando fórmula do produto misto para o volume do tetraedro

Fazendo a origem no vértive A do cubo teremos:

[latex]\\ K = 1,0,0\\ J = 0,2,1\\ G = 2,2,2\\ I = 0,1,2\\ \overrightarrow {u} = \overrightarrow {KJ} = J-K =(-1,2,1)\\ \overrightarrow {v} = \overrightarrow {KG} = G-K =(1,2,2)\\ \overrightarrow {w} = \overrightarrow {KI} = I-K =(-1,1,2)\\ V=\frac{1}{6}\cdot\begin{Vmatrix} -1 &2 &1 \\ 1 &2 &2 \\ -1& 1 &2 \end{Vmatrix}=\frac{1}{6}\cdot|-7|=\boxed{\frac{7}{6}} [/latex]

(Solução:Prof. Victor)

por mhope Seg 15 Ago 2022, 09:12

Também resolvi por R3, mas queria entender por geometria espacial. Se alguém souber, ajude por favor!

por **petras** Seg 15 Ago 2022, 10:27

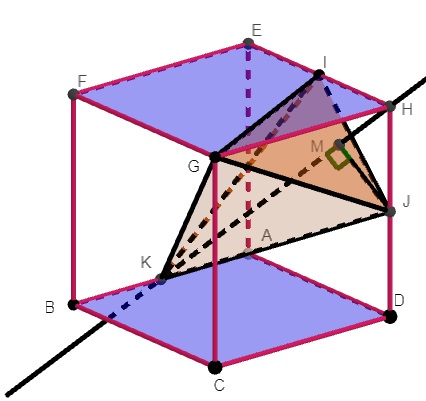
[latex]Base_p:\triangle GIJ\\ \triangle GHJ: GJ^2=1^2+2^2\implies GJ= \sqrt5\\ \triangle GIH: GI^2=1^2+2^2 \implies GI=\sqrt5\\ \triangle HIJ: IJ^2=1^2+1^2 \implies IJ = \sqrt2\\ h_{\triangle {GIJ}}: h^2= \sqrt5^2-(\frac{\sqrt2}{2})^2\implies h = \frac{3\sqrt2}{2} \\ \therefore S_{\triangle {GIJ}}=\frac{1}{2}.\frac{3\sqrt2}{2}.\sqrt2=\underline {\frac{3}{2}}\\ H_p=KM\\ \triangle AKD:KD = \sqrt{2^2+1^2} = \sqrt5 \\ \triangle KDJ: KJ=\sqrt{1^2+\sqrt5^2}=\sqrt6\\ \triangle KHD: KH^2= \sqrt{2^2+\sqrt5^2}=3\\ \triangle JMH: Sendo~MH=x\implies JM^2 = x^2-1^2\\ \triangle JKM: JM^2 = \sqrt6^2-(3-x)^2 \\ Igualando: x^2-1^2 = 6-9+6x-x^2 \implies x = \frac{2}{3}\\ \therefore KM = 3-\frac{2}{3} =\underline{ \frac{7}{3}}\\ \therefore V_p = \frac{1}{3}.\frac{3}{2}.\frac{7}{3}=\boxed{\frac{7}{6}}\color{green}\checkmark [/latex]