Unicamp 2022 - PA e Geometria Plana
2 participantes
Página 1 de 1
Unicamp 2022 - PA e Geometria Plana
por Ana Laura Guimarães Ter 26 Abr 2022, 16:02
Um círculo está inscrito em um quadrilátero ABCD. Seja T o ponto de tangência do lado DA com o círculo. Sabe-se que as medidas dos lados AB, BC e CD formam, nesta ordem, uma progressão aritmética crescente de números inteiros e que a medida do lado DA é 3. Considerando que a medida do segmento TA é um número inteiro, as medidas dos lados AB, BC e CD são, respectivamente:
A ) 1, 3, 5
B ) 2, 3, 4
C ) 2, 4, 6
D ) 3, 4, 5
- GABARITO:
- B
Boa tarde, poderiam me explicar como resolver essa questão? 
Última edição por Ana Laura Guimarães em Ter 26 Abr 2022, 16:56, editado 1 vez(es)
Ana Laura Guimarães- Mestre Jedi
- Mensagens : 945
Data de inscrição : 12/02/2021
Localização : Belo Horizonte - Minas Gerais -
Re: Unicamp 2022 - PA e Geometria Plana
por Fibonacci13 Ter 26 Abr 2022, 16:16
Olá Ana, achei uma resolução. Espero que te ajude.
Uma questão interessante de geometria plana, onde utilizaremos o Teorema de Pitot. Vamos ilustrar o círculo e o quadrilátero propostos no enunciado.
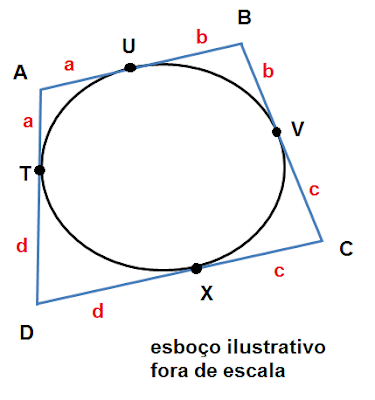
De acordo com o Teorema de Pitot: se um quadrilátero é circunscritível, então a soma dos lados opostos tem que ser igual, ou seja,
DA + BC = AB + CD
Do enunciado, sabemos que AB, BC e CD formam, nesta ordem, uma progressão aritmética crescente de números inteiros, logo, temos
AB = a1
BC = a1 + r
CD = a1 + 2r
DA = 3
DA + BC = AB + CD
3 + a1 + r = a1 + a1 + 2r
3 = a1 + r
Repare que BC = a1 + r = 3, com isso, para satisfazer o Teorema de Pitot, a PA de números inteiros só pode ter as seguinte medidas:
{ AB, BC, CD } = { 1, 3, 5 } ou { 2, 3, 4 }
Mas tem um detalhe importante no enunciado: "considerando que a medida do segmento TA é um número inteiro". Veja na figura que AT = AU e com isso, o lado AB não poderia valer 1, pois forçaria o valor de "a" ser um valor fracionário. Com isso, o lado AB tem que valer 2. Finalmente, a PA é dada por {2, 3, 4 }.
Alternativa correta é a letra b).
Resolução:
Uma questão interessante de geometria plana, onde utilizaremos o Teorema de Pitot. Vamos ilustrar o círculo e o quadrilátero propostos no enunciado.
De acordo com o Teorema de Pitot: se um quadrilátero é circunscritível, então a soma dos lados opostos tem que ser igual, ou seja,
DA + BC = AB + CD
Do enunciado, sabemos que AB, BC e CD formam, nesta ordem, uma progressão aritmética crescente de números inteiros, logo, temos
AB = a1
BC = a1 + r
CD = a1 + 2r
DA = 3
DA + BC = AB + CD
3 + a1 + r = a1 + a1 + 2r
3 = a1 + r
Repare que BC = a1 + r = 3, com isso, para satisfazer o Teorema de Pitot, a PA de números inteiros só pode ter as seguinte medidas:
{ AB, BC, CD } = { 1, 3, 5 } ou { 2, 3, 4 }
Mas tem um detalhe importante no enunciado: "considerando que a medida do segmento TA é um número inteiro". Veja na figura que AT = AU e com isso, o lado AB não poderia valer 1, pois forçaria o valor de "a" ser um valor fracionário. Com isso, o lado AB tem que valer 2. Finalmente, a PA é dada por {2, 3, 4 }.
Alternativa correta é a letra b).
Fibonacci13- Mestre Jedi
- Mensagens : 872
Data de inscrição : 14/09/2019
Idade : 22
Localização : São Paulo
Ana Laura Guimarães gosta desta mensagem
Re: Unicamp 2022 - PA e Geometria Plana
por Ana Laura Guimarães Ter 26 Abr 2022, 16:44
Perfeito, muito obrigada pela resolução , estava tendo dificuldade de entender a parte onde não pode ser 1, porém, agora peguei o raciocínio, se o lado todo for 1, o pedaço TA teria que ser fracionado.
o Teorema de Pitot é bem útil, não me lembrava dele.
Legal frisar também a propriedade das retas tangentes para que TA = AU
o Teorema de Pitot é bem útil, não me lembrava dele.
Legal frisar também a propriedade das retas tangentes para que TA = AU
Ana Laura Guimarães- Mestre Jedi
- Mensagens : 945
Data de inscrição : 12/02/2021
Localização : Belo Horizonte - Minas Gerais -
Tópicos semelhantes» Fuvest 2022 - Geometria Plana
» Fuvest 2022 - Geometria Plana: Circunferência
» Geometria plana - São Camilo 2022 Medicina
» (UFRGS-2022) Geometria Plana, arcos de circunferência
» unicamp - geometria plana
» Fuvest 2022 - Geometria Plana: Circunferência
» Geometria plana - São Camilo 2022 Medicina
» (UFRGS-2022) Geometria Plana, arcos de circunferência
» unicamp - geometria plana
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
