Gráfico de função Afim e quadrática

Considere a figura a seguir, em que estão representados os gráficos de uma função quadrática e de uma função linear.


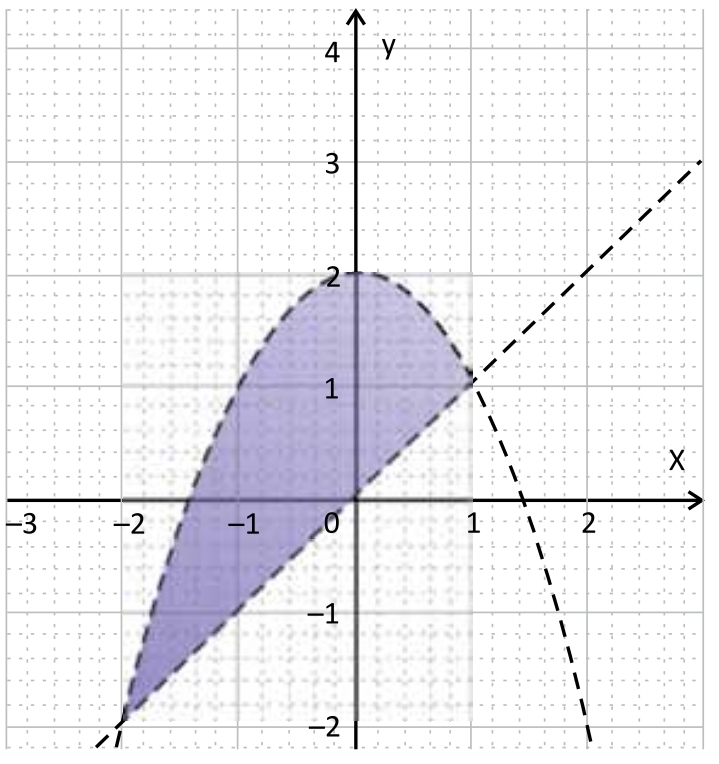
A região hachurada corresponde a
(A) x < y < –[latex]x^{2}[/latex] + 2
(B) –[latex]x^{2}[/latex] + 2 < y < x
(C) x < y < [latex]x^{2}[/latex] – 2
(D) [latex]x^{2}[/latex] – 2 < y < x
(E) –x < y < [latex]x^{2}[/latex] – 4

Gab: A

Quem puder explicar para mim a questão eu agradeço muito, não entendi como resolver.

Olá Amanda;

Podemos determinar as duas funções que representam as curvas da parábola e da reta, começando pela parábola, temos que pela teoria é do tipo f(x) = ax² + bx + c, mas perceba que c = 2, onde corta o eixo das ordenadas. Para calcular a e b vamos utilizar de que:



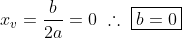
Pronto precisamos determinar o parâmetro a.

Para calcular o parâmetro a precisamos montar um sistema, mas para isso vamos usar a reta dada no gráfico. É fácil perceber que a reta é do tipo g(x) = x, uma reta linear, ou seja, temos valores de imagens iguais para abscissas iguais. Um dos pontos de intersecção da reta com a parábola é (-2,-2), logo:



Obs: Poderia ter utilizado de maneira análoga para o ponto (1,1).

Nossa equação da parábola é do tipo:



Chegamos que a região do intervalo é demarcada entre os pontos de intersecção f(x) e g(x), onde apresenta o máximo com f(x) e o mínimo com g(x):



Letra A. Espero ter ajudado!