Maior área possível em função de x

por Henrique de Cristo Ter 10 Nov 2020, 19:41

Um empresário pretende em sua boate de 36km2 de área fazer uma reforma de modo que possa alterar o tamanho da pista de dança e limitar ao máximo as áreas do banheiro e bar. Na figura a seguir, temos um pequeno esboço do projeto que seu engenheiro propôs.

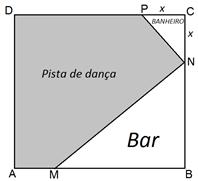
Maior área possível em função de x KvaG9fCwvCZLpHKtetCErucAaeqHEiXr2f9C4cCDiDc_-nholeF9zn_K5BtqA5nA2RVrUCqnZxeDbR4GMJmisfVIUU3PcVcf40KkckRSPG6D-STOrmVqa2mJbE40ag=w198

Maior área possível em função de x KvaG9fCwvCZLpHKtetCErucAaeqHEiXr2f9C4cCDiDc_-nholeF9zn_K5BtqA5nA2RVrUCqnZxeDbR4GMJmisfVIUU3PcVcf40KkckRSPG6D-STOrmVqa2mJbE40ag=w198

Não contente com o projeto, pretende saber o valor de x para que a pista de dança seja máxima. Então o engenheiro, após alguns cálculos, verificou que quando:
a) x = 3, a pista de dança possui maior área.
b) x = 2, a pista de dança possui maior área.
c) x = 6, a pista de dança possui maior área.
d) x = 9, a pista de dança possui maior área.
e) x = 1, a pista de dança possui maior área.

Gab.: Letra A.

por **Elcioschin** Ter 10 Nov 2020, 22:21

S = 36 ---> lado do quadrado = 6

CN = CP = AM = x ---> BM = BN = 6 - x

S(ban) = x²/2 ---> S(bar) = (6 - x)²/2

S(dan) = 36 - S(ban) - S(bar)

Substitua e chegue numa função do 2º grau (parábola com concavidade voltada para baixo:

Calcule xV