Circunferência

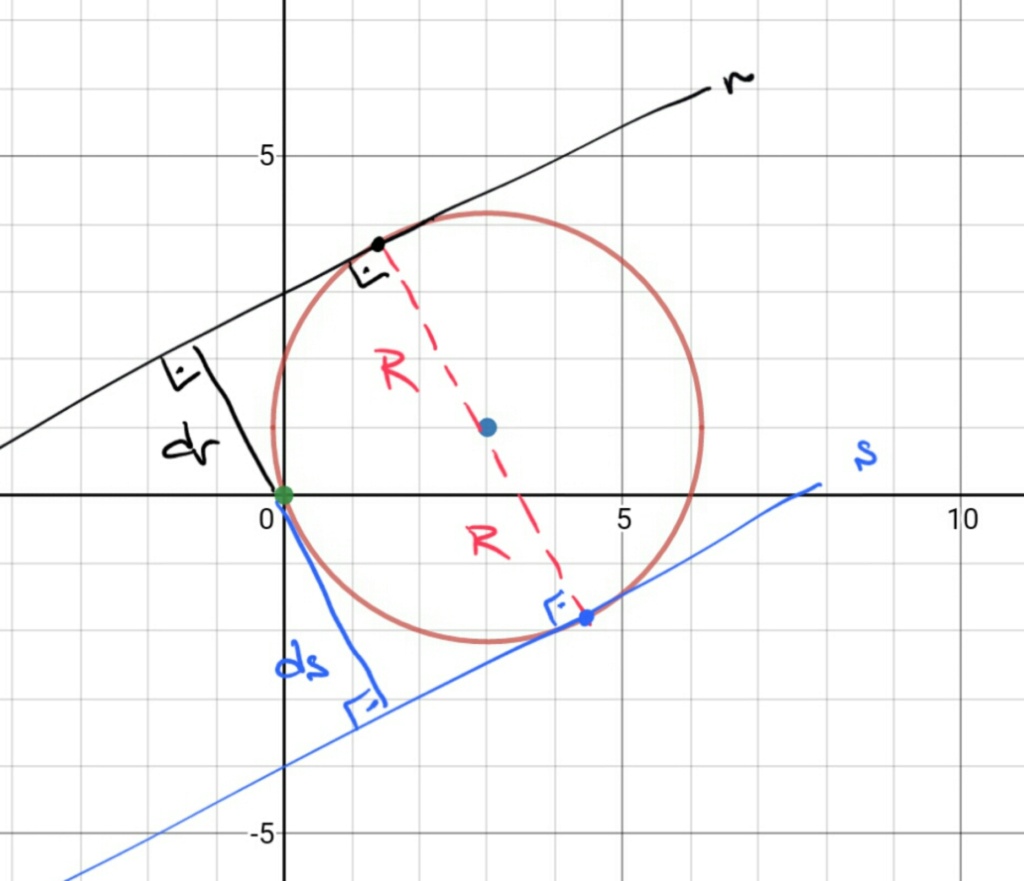
As retas paralelas r e s são tangentes à circunferência de equação x²+y²-6x-2y=0. Sendo dr a distância da reta r a origem do sistema de coordenadas cartesianas e ds, a distância da reta s a esse mesmo ponto, pode-se afirmar que dr + ds é igual a:

a) 3
b) 3√3
c) 6
d) 2√10
e) 6√2

gostaria da resposta com desenho da resolução, obg!

esta circunferência tem centro C=(3, 1), raio R=√10 e passa pela origem (0, 0).

as retas r e s são paralelas e tangentes à circunferência, portanto ou são diametralmente opostas.
Obs.: quando falam em "retas paralelas" entende-se que podem também ser coincidentes. Não gosto desta consideração mas o meu gosto não importa. O fato é que isto não vale para o gabarito desta questão.

o ponto de tangência de r e s faz ângulo reto com um mesmo único diâmetro, pois são restas diametralmente opostas. E a distância à origem, d_r e d_s é medida na perpendicular a essas retas. Portanto os segmentos dessas distâncias são paralelos ao diâmetro definido pelos pontos de tangências citados e consequentemente estão alinhados. Então a soma dessas distâncias é igual ao diâmetro da circunferência, ou seja


Note que não importa qual a declividade das retas nem o ponto em que tocam a circunferência que a soma das distâncias será sempre 2.R -- mesmo que uma delas passe pela própria origem.