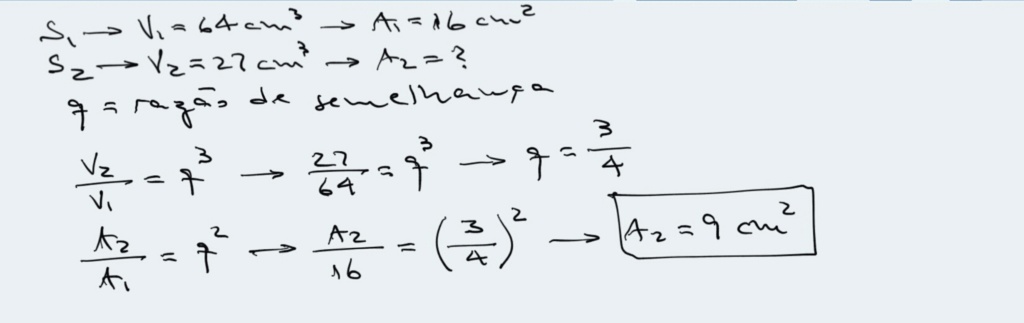Semelhança entre sólidos
4 participantes
Página 1 de 1
 Semelhança entre sólidos
Semelhança entre sólidos
Dois sólidos semelhantes, S[size=11]1
e S2, tem seus volumes respectivamente iguais a 64 cm3 e 27 cm3. Sabendo que a área total de S1 mede 16 cm2, qual a área total, em cm2, de S2?
[size=15]a.
6
b.
9
c.
12
d.
16
e.
21[/size][/size]
Eu fiz : (64/27)=(16/x)² (64/27)=[(256)/(x²)] ----> 108=x² ----> Dá um número quebrado.... Gostaria de saber em que ponto estou errando.

zwelonu- Padawan

- Mensagens : 87
Data de inscrição : 13/08/2019
Idade : 22
Localização : Rio de Janeiro,RJ,Brasil
 Re: Semelhança entre sólidos
Re: Semelhança entre sólidos
Seja L um lado do sólido de maior volume e l um lado do sólido de menor volume .
L e l são correspondentes.
A razão de semelhança é :
(L/l)^3= 64/27 (1)
Para áreas temos:
(L/l)^2=16/x (2)
Elevando ao quadrado 1 e ao cubo 3 , rm seguida igualando temos:
(16/x)^3=(64/27)^2
(16/x)^3=(4/3)^3)^2
(16/x)^3=(4/3)^6
Elevando a 1/3ambos os lados temos:
(16/x)=(4/3)^2
(16/x)=(16/9) --> x=9cm
L e l são correspondentes.
A razão de semelhança é :
(L/l)^3= 64/27 (1)
Para áreas temos:
(L/l)^2=16/x (2)
Elevando ao quadrado 1 e ao cubo 3 , rm seguida igualando temos:
(16/x)^3=(64/27)^2
(16/x)^3=(4/3)^3)^2
(16/x)^3=(4/3)^6
Elevando a 1/3ambos os lados temos:
(16/x)=(4/3)^2
(16/x)=(16/9) --> x=9cm

Emersonsouza- Fera

- Mensagens : 1100
Data de inscrição : 14/01/2015
Idade : 28
Localização : Rio de Janeiro

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Re: Semelhança entre sólidos
Re: Semelhança entre sólidos
Você tem que pensar que a relação entre as alturas aparece nas duas equações
(h/H)^3 = (S2/S1)
(h/H)^2 = (A2/A1)
S2 = volume do sólido 2
S1 = volume do sólido 1
A1 = área do sólido 1
A2 = área do sólido 2
Como são sólidos semelhantes (ou seja, um não pode ter uma altura pequena e um volume maior do que o outro de altura maior porque suas dimensões seguem uma proporção), o sólido de maior volume terá a maior altura, por isso S1 fica no denominador em S2/S1 assim como H fica no denominador em h/H.
(h/H)^3 = (S2/S1)
h/H = ∛(S2/S1) =
(h/H)^2 = (A2/A1)
h/H = √(A2/A1) =
Como a relação h/H é a mesma, basta igualar os termos







A2 = 9 cm^2
(h/H)^3 = (S2/S1)
(h/H)^2 = (A2/A1)
S2 = volume do sólido 2
S1 = volume do sólido 1
A1 = área do sólido 1
A2 = área do sólido 2
Como são sólidos semelhantes (ou seja, um não pode ter uma altura pequena e um volume maior do que o outro de altura maior porque suas dimensões seguem uma proporção), o sólido de maior volume terá a maior altura, por isso S1 fica no denominador em S2/S1 assim como H fica no denominador em h/H.
(h/H)^3 = (S2/S1)
h/H = ∛(S2/S1) =
(h/H)^2 = (A2/A1)
h/H = √(A2/A1) =
Como a relação h/H é a mesma, basta igualar os termos
A2 = 9 cm^2
Nickds12- Mestre Jedi

- Mensagens : 577
Data de inscrição : 31/08/2019
Idade : 27
Localização : RJ
 Tópicos semelhantes
Tópicos semelhantes» Semelhança entre sólidos
» Razão de semelhança entre sólidos não serve para esfera
» Semelhança de sólidos (cones)
» Geometria espacial semelhança sólidos
» (FGV-SP) Atrito entre sólidos
» Razão de semelhança entre sólidos não serve para esfera
» Semelhança de sólidos (cones)
» Geometria espacial semelhança sólidos
» (FGV-SP) Atrito entre sólidos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos