Área do octógono

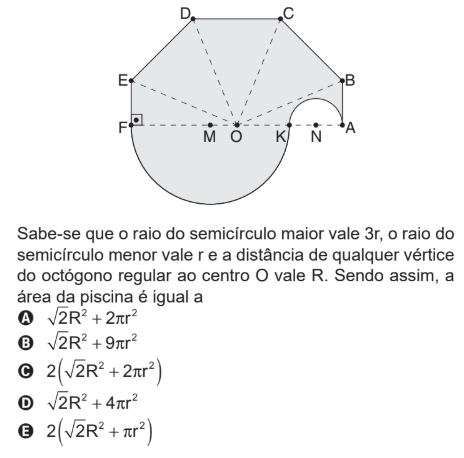
Um arquiteto projetou uma piscina inovadora, combi-
nando um octógono regular com dois semicírculos. Ao tra-
çar a mediatriz de um dos lados, ele dividiu o octógono ao

meio, criando o segmento AF. Na nova base AF, marcou-se
o ponto médio O e, em seguida, no segmento AO, o ponto
médio K. No segmento FK, marcou-se o ponto médio M,
sendo FM o raio do semicírculo maior. No segmento AK,

marcou-se o ponto médio N, sendo AN o raio do semicírcu-
lo menor. A figura a seguir representa o projeto da piscina.

Spoiler:

???Por que fica errado quando eu cálculo a área do triângulo do octógono pela lei dos cossenos???

Não sabemos pois você não mostrou o passo-a-passo da sua solução.

Dicas:

Seja R = OB = OC = OD = OE e seja L = BC = CD = DE 
Seja P o ponto médio de CD = PC = AB = EF = L/2
Seja a = OP = OA = OE o apótema do octógono

OA = a ---> OK = AK = a/2 ---> NK = NA = a/4 ---> I

AF = OA + OF ---> AF = a + a ---> AF = 2.a ---> OA = OF = a

FK = OF + OK ---> FK = a + a/2 ---> FK = 3.a/2

MF = MK = FK/2 ---> MF = MK = (3.a/2)/2 --->  MF = MK = 3.a/4

MF = 3.r ---> 3.a/4 = 3.r ---> a = 4.r

I ---> NK = NA = a/4 ---> NK = NA = (4.r/4) ---> NK = NA = r

OC² = PC² + OP² ---> R² = (L/2)² + a² ---> R² = L²/4 + (4.r)² --> R² = L²/4 + 16.r² --->

L² = 4.R² - 64.r²

Área de OCD ---> s = R².sen(CÔD)/2 ---> s = R².sen45º/2 ---> Calcule em função de R, r

Área de metade do octógono ---> S = 4.s ---> Calcule s

Calcule as áreas de cada semicírculo e complete a questão.

Elcioschin escreveu:
Área de OCD ---> s = R².sen(CÔD)/2 ---> s = R².sen45º/2 ---> Calcule em função de R, r

Área de metade do octógono ---> S = 4.s ---> Calcule s

Quando você calculou a área do triângulo OCD, usou a lei dos senos.
Eu considerei um triângulo de ângulo 45o, ok, e lados R e R e a altura o segmento FO (3r)

Mas pela lei dos cossenos, base X
X²= 2R² - √2R² 
X = √(2-√2)R
 
Área de OCD: X.FO/2


Não fica igual

Suponho que o seu X seja o lado L do octógono

X² = R² + R² - 2.R.R.cos45º ---> X² = 2.R² - √2.R² ---> X = √(2 - √2).R


S(BOC) = X.FO/2 ---> Faltou você continuar, colocando no lugar de FO o valor do apótema

S = √(2 - √2).R.4r / 2  
S =  2√(2 - √2).Rr --> (Achei que sairia o mesmo √2R² achado pela lei dos senos).  A partir daqui não saberia o que fazer.


Os outros elementos encontrei a área e soube como cálcular o total. Meu problema foi com o triângulo mesmo

Raquel,

também dá certo, embora muito mais trabalhoso; é preciso apenas atenção a detalhes.


usei Pitágoras para achar a medida de FO.