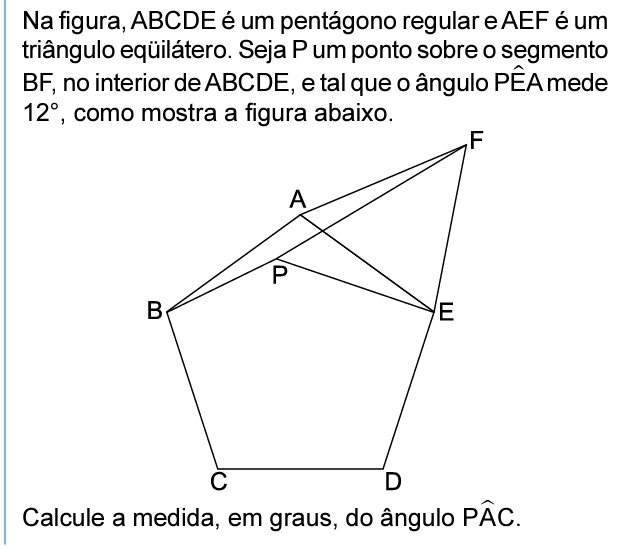
Polígonos - Geometria plana
2 participantes
Página 1 de 1
NMS50- Recebeu o sabre de luz

- Mensagens : 107
Data de inscrição : 04/03/2019
Idade : 24
Localização : Suzano, Sao Paulo, Brasil
 Re: Polígonos - Geometria plana
Re: Polígonos - Geometria plana
O problema é essencialmente de marcar ângulos e atentar aos triângulos isósceles que aparecem, entretanto não indiquei tudo pois o desenho do enunciado ficou péssimo para a resolução, acompanhe os passos lendo:
Como um dos lados do △AEF equilátero também é lado do polígono regular, todos os lados dele são também iguais aos do triângulo, logo △BAF é isósceles.
∠BAE é um ângulo interno do pentágono regular, sabemos que vale 108°, portanto ∠BAF será 108° + 60° = 168°, e ∠ABF = ∠AFB = 6° por soma interna.
Marcando os ângulos perto do △AEF, temos que ∠BFE = 60° - 6° = 54°. Utilizando agora o dado da questão, sabemos que ∠PEA mede 12°, olhando para △PFE encontramos que ∠EPF deve ser então 54° para satisfazer a soma interna. Nesse momento você deve notar que ∠EFP = ∠EPF = 54° e, portanto, △PFE é isósceles, pois dessa maneira consegue ver que △PEA também será (triângulo azul na figura), e sabemos o ângulo de seu vértice ∠PEA = 12°, logo ∠EPA = ∠EAP = 84° por soma interna.
Agora algo mais difícil de perceber: veja que △BAC é isósceles (triângulo verde na figura), sabemos que ∠ABC é interno do pentágono, 108°, e por soma interna ∠BCA = ∠BAC = 36°. Olhe para o ângulo ∠BAE = 108° e veja que ele é composto pelos ângulos ∠BAC e ∠CAE, mas ∠CAE é justamente o ângulo ∠EAP = 84° do isósceles △PEA menos o ângulo ∠PAC que queremos, assim podemos montar uma equação:
∠BAE = ∠BAC + ∠EAP - ∠PAC
108° = 36° + 84° - ∠PAC
∠PAC = 12°
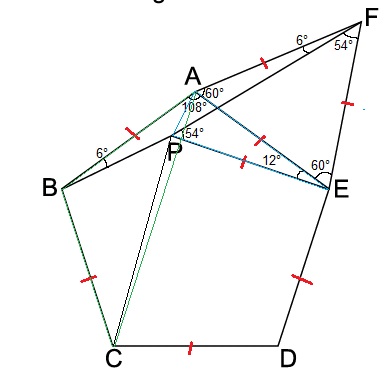
Como um dos lados do △AEF equilátero também é lado do polígono regular, todos os lados dele são também iguais aos do triângulo, logo △BAF é isósceles.
∠BAE é um ângulo interno do pentágono regular, sabemos que vale 108°, portanto ∠BAF será 108° + 60° = 168°, e ∠ABF = ∠AFB = 6° por soma interna.
Marcando os ângulos perto do △AEF, temos que ∠BFE = 60° - 6° = 54°. Utilizando agora o dado da questão, sabemos que ∠PEA mede 12°, olhando para △PFE encontramos que ∠EPF deve ser então 54° para satisfazer a soma interna. Nesse momento você deve notar que ∠EFP = ∠EPF = 54° e, portanto, △PFE é isósceles, pois dessa maneira consegue ver que △PEA também será (triângulo azul na figura), e sabemos o ângulo de seu vértice ∠PEA = 12°, logo ∠EPA = ∠EAP = 84° por soma interna.
Agora algo mais difícil de perceber: veja que △BAC é isósceles (triângulo verde na figura), sabemos que ∠ABC é interno do pentágono, 108°, e por soma interna ∠BCA = ∠BAC = 36°. Olhe para o ângulo ∠BAE = 108° e veja que ele é composto pelos ângulos ∠BAC e ∠CAE, mas ∠CAE é justamente o ângulo ∠EAP = 84° do isósceles △PEA menos o ângulo ∠PAC que queremos, assim podemos montar uma equação:
∠BAE = ∠BAC + ∠EAP - ∠PAC
108° = 36° + 84° - ∠PAC
∠PAC = 12°


lookez- Recebeu o sabre de luz

- Mensagens : 140
Data de inscrição : 11/10/2018
Idade : 24
Localização : RJ, RJ, Brasil
 Re: Polígonos - Geometria plana
Re: Polígonos - Geometria plana
Muito obrigada!!!
NMS50- Recebeu o sabre de luz

- Mensagens : 107
Data de inscrição : 04/03/2019
Idade : 24
Localização : Suzano, Sao Paulo, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Geometria Plana - Polígonos
» Geometria plana - polígonos
» Geometria Plana - Polígonos
» Geometria Plana - Polígonos
» Geometria Plana - Polígonos
» Geometria plana - polígonos
» Geometria Plana - Polígonos
» Geometria Plana - Polígonos
» Geometria Plana - Polígonos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos