UnB 2° Dia 2009/1

A razão áurea é uma relação matemática definida algebricamente pela expressão 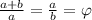, em que a e b representam  números, e 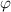, uma constante de valor aproximado igual a 1,618. Na figura acima, são apresentadas situações em que está presente a razão áurea, que, por traduzir beleza e harmonia, é também encontrada na arquitetura, nas artes visuais e, muito frequentemente, na música. A característica comum dessas obras de arte é que, a partir do ponto focal ou clímax, é possível definir elementos no tempo, como na música, ou no espaço, como na pintura e na fotografia, que respeitam à razão áurea. Na estrutura da forma sonata do período clássico, por exemplo, o clímax divide o intervalo do tempo total da música em duas partes a e b que obedecem à razão áurea.


A partir dessas informações, julgue o item a seguir.
Considere que um geômetra-músico, ao compor uma música, tenha associado todo o intervalo de tempo que antecede ao clímax a um comprimento a, que utilizou posteriormente para construir um quadrado de lado a, como mostrado na figura a seguir. Ele, então, a partir do ponto P que divide a base do quadrado em dois segmentos iguais, traçou o segmento de reta PQ, como mostrado na figura. Em seguida, obteve o segmento de comprimento b, fazendo com que os pontos Q e R pertençam ao arco de circunferência de raio PQ, conforme mostrado na figura. Sabendo-se, ainda, que a + b corresponde ao intervalo de tempo total da música, conclui-se que essa música com o clímax assim definido tem a estrutura da forma sonata do período clássico.



a) CERTO
b) ERRADO

(a + b)/a = a/b ---> a.b + b² = a² ---> b² + a.b - a² = 0 ---> : a²

(b/a)² + b/a - 1 = 0 ---> Equação do 2º grau na variável b/a

∆ = 1² - 4.1.(-1) ---> ∆ = 5

Raiz positiva---> b/a = (√5 - 1)/2

Na figura: PQ² = a² + (a/2)² ---> PQ² = a².5/4 ---> PQ = a.√5/2

PR = PQ ---> a/2 + b = a.√5/2 ---> b = a.√5/2 - a/2 ---> : a ---> b/a = (√5 - 1)/2

a) CERTO

Já tinha feito, vou postar...

Mas por que é a) CERTO?

Acho que eu não entendi qual é a pergunta dessa questão.

E para o Francisco+1, de onde veio o a^2 que surgiu depois de a/2 + b = r? Parece que o b elevado ao quadrado resultou em a^2, mas não entendo como poderia ser assim

1) Ele queria saber se o desenho atendia a relação áurea. Provamos que sim.

2) O a² não tem nada a ver com a/2 + b = r

Ele simplesmente aplicou Pitágoras no triângulo retângulo: PQ² = (a/2)² + a² ---> r² = (a/2)² + a²