Questão sobre tangente

(G1 - cmrj 2019) Os alunos do 9º ano do CMRJ foram a uma visita ao Palácio Duque de
Caxias para, além de conhecer o palácio, executar um trabalho sobre “grandes medições”,
solicitado pelo seu professor de Matemática.
Os alunos tinham que estimar a altura do prédio da Central do Brasil localizado ao lado do
Palácio Duque de Caxias. Para realizar a tarefa, os alunos teriam que fazer a medição de
ângulos a partir de três pontos distintos, determinados pelo professor, com o auxílio de um
teodolito e utilizar raiz de 3 =1, 7 3
em seus cálculos.
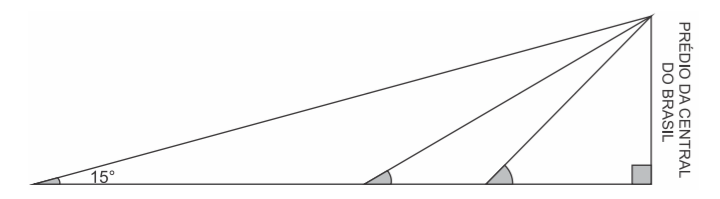
Observe os resultados obtidos com as três medições descritas a seguir:
- a primeira medição foi feita a uma distância de
4 1 0 m
do prédio, e o topo do prédio foi
observado segundo um ângulo de
1 5 ; 
- a segunda medição foi feita depois de se aproximar do prédio, e o ângulo observado foi o
dobro do ângulo da primeira medição;
- a terceira medição foi feita depois de se aproximar
8 4 m
do prédio, a partir do ponto da
segunda medição, e o ângulo observado foi o triplo do ângulo da primeira medição.



A) 34 m
B) 48 m
C)79 m
D) 115 m
E) 121 m

Fiz a questão da seguinte maneira:
Calculei a tangente de 15° (60°-45°), que, substituindo pelo valor de raiz de três sugerido na questão, resultou em 0,73/2,73.
Depois, fiz tg 15°=0,73/2,73 = h/410
Nesse caso, calculei o resultado aproximado de 109,6 m para h. Porém, esse valor não se encontra dentre as alternativas. Alguém poderia me apontar onde estou errando? Já revi os cálculos inúmeras vezes e não consigo encontrar o erro.

estudantededicada2017, você está violando uma das regras do fórum.
"IX- As questões devem ser postadas em modo texto, não sendo aceitas imagens ou links para o enunciado da questão. São aceitas imagens para adicionar figuras esclarecedoras ou que façam parte da questão. Isto se deve ao fato de que os mecanismos de busca, tanto internos quanto externos não reconhecem imagens."
Por favor,edite a postagem para podermos  te ajudar.

Mensagem editada.

devido ao ângulo de 45°, o triângulo VCP é retângulo isósceles e portanto VP=CP --> h=x

Porém podia ser calculado com apenas a primeira medição.

\\\tan 15^{\circ} = \frac{\sin 15^{\circ}}{cos 15^{\circ}} = \frac{h}{410} \\\\
\therefore \frac{h}{410} = \frac{\frac{\sqrt{6}-\sqrt{2}}{4}}{\frac{\sqrt{6}+\sqrt{2}}{4}} \to \frac{h}{410} = \frac{\left (\sqrt{6}-\sqrt{2} \right )^2}{6-2}\\\\
h = 410 \cdot \frac{6+2-2.2.\sqrt{3}}{4} = 410 \cdot \left (2-\sqrt{3} \right ) = 410 \cdot (2-1,73)\\\\
h = 410\cdot 0,27 = 110,7 \approx 111 \; m

Como o cálculo anterior resultou em aprox. 115 m, podemos concluir que a leitura do ângulo de 15°, por ser um ângulo pequeno (muito agudo) é mais difícil tornando-a mais imprecisa.

Entendi. Muito obrigada!