Determinar o valor de:

por Igor Kauan Souza da Mata Qui 09 maio 2019, 19:24

Oi, gente! Tudo bem? Vocês conseguem me ajudar com essa?

Determinar o valor de:
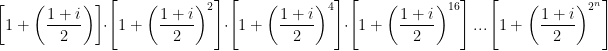
$Determinar o valor de: Gif.latex?%5Cdpi%7B100%7D%20%5Cleft%5B1+%5Cleft%28%5Cfrac%7B1+i%7D%7B2%7D%20%5Cright%20%29%20%5Cright%20%5D%5Ccdot%5Cleft%5B1+%5Cleft%28%5Cfrac%7B1+i%7D%7B2%7D%20%5Cright%20%29%5E2%20%5Cright%20%5D%5Ccdot%5Cleft%5B1+%5Cleft%28%5Cfrac%7B1+i%7D%7B2%7D%20%5Cright%20%29%5E4%20%5Cright%20%5D%5Ccdot%5Cleft%5B1+%5Cleft%28%5Cfrac%7B1+i%7D%7B2%7D%20%5Cright%20%29%5E%7B16%7D%20%5Cright%20%5D..$

Alternativas

$Determinar o valor de: Gif$
$Determinar o valor de: Gif$ (Alternativa Correta)
$Determinar o valor de: Gif$
$Determinar o valor de: Gif$
$Determinar o valor de: Gif$

por **fantecele** Qui 09 maio 2019, 19:33

Opa, tudo bem?

Agora tá meio ruim pra fazer a questão, mas a idéia é multiplicar e dividir por (1 - (1+i)/2) e usar a idéia de (a-b)(a+b) = (a^2 - b^2), só fazer isso que sai.

por Igor Kauan Souza da Mata Qui 09 maio 2019, 21:28

Não consegui fazer assim, devo ter me confundido em alguma coisa... Pode me ajudar desenvolver?

por **Elcioschin** Qui 09 maio 2019, 21:48

a) (1 + i)² = 1 + 2.i + i² ---> (1 + i)² = 1 + 2.i - 1 ---> (1 + i)² = 2.i --->

b) [(1 + i)/2]² = (1 + i)²/2² = (2.i)/4 = i/2

c) [(1 + i)/2]⁴ = {[(1 + i)/2]²}² = (i/2)² = -1/4

d) [(1 + i)/2]⁸ = {[(1 + i)/2]⁴}² = (-1/4)² = 1/16

E assim por diante
Notem que a partir de c) o resultado é um número real

Os produtos dois 2 primeiros fatores vale:

{1 + [(1 + i)/2]}.{1 + [(1 + i)/2]²} = (3/2 + i/2).(1 + i/2) = (5/4).(1 + i)

O 3º fator vale ---> 1 - 1/4 = 3/4 = 12/16
O 4º fator vale 1 + 1/16 = 17/6

Tente completar calculando os demais fatores

por **fantecele** Qui 09 maio 2019, 22:20

Então, aparentemente o látex não quer funcionar aqui, vou ter que fazer digitando, qualquer coisa depois eu tento mudar para o látex, e qualquer coisa ai é só perguntar:

Primeiro multiplique e divida por (1 - (1+i)/2), dai par ao primeiro termo da multiplicação iremos ter que:

(1 - (1+i)/2).(1 + (1+i)/2) = (1 - ((1+i)/2)^2)

Para o segundo termo:

(1 - ((1+i)/2)^2).(1 + ((1+i)/2)^2) = (1 - ((1+i)/2)^(2^2))

Para o terceiro termo:

(1 - ((1+i)/2)^(2^2)).(1 + ((1+i)/2)^(2^2)) = (1 - ((1+i)/2)^(2^3))

Perceba que para o primeiro termo tinhamos 2^0 e foi para 2^1, para o segundo foi do 2^1 para o 2^2, o terceiro foi do 2^2 para 2^3, continuando assim até o último termo, iremos chegar em:

(1 - ((1+i)/2)^(2^(n+1)))

Dessa forma aquele produto é igual a:

(1 - ((1+i)/2)^(2^(n+1)))/(1 - (1+i)/2)

Primeiro para o x/(1 - (1+i)/2), temos que: x = (1 - ((1+i)/2)^(2^(n+1)))

x/(1 - (1+i)/2) = x/(1 - i)/2 = 2x/(1-i) = (1+i)x

Agora manipulando ((1+i)/2)^(2^(n+1)):

((1+i)/2)^(2^(n+1)) = (((1+i)/2)^2)^(2^n) = (-1/2)^(2^n) = 1/2^(2^n)

(1 - ((1+i)/2)^(2^(n+1))) = (1 - 1/2^(2^n))

(1+i).x = (1+i).(1 - 1/2^(2^n))

Acabei chegando nisso ai, aparentemente não chegou no gabarito.

Qualquer coisa ai é só perguntar.