Puc - 2017
3 participantes
Página 1 de 1
Puc - 2017
por Gandalf_o_BRanco Qui 21 Fev 2019, 11:21
(PUCPR 2017) Em uma divisão, a soma do resto r, divisor d e dividendo D é 178. Se o quociente é 7 e o resto é o maior valor possível, qual o valor da soma do dividendo com o resto?
R = 160
R = 160
Última edição por Gandalf_o_BRanco em Qui 21 Fev 2019, 21:21, editado 1 vez(es)
Gandalf_o_BRanco- Padawan
- Mensagens : 84
Data de inscrição : 01/03/2018
Re: Puc - 2017
por Emanuel Dias Qui 21 Fev 2019, 13:31
https://pir2.forumeiros.com/t71268-problema-do-1-espcex de uma olhada aqui, é basicamente a mesma quesão, só muda os números.
Última edição por endis7 em Qui 21 Fev 2019, 16:12, editado 1 vez(es)
Emanuel Dias- Monitor
- Mensagens : 1722
Data de inscrição : 15/12/2018
Idade : 23
Localização : São Paulo
Re: Puc - 2017
por Paduan Qui 21 Fev 2019, 13:54
Temos o esquema da divisão por chaves a seguir:
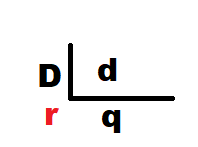
Daí,
1 - q.d + r = D ( da divisão como um todo)
2 - r + d + D = 178 (do enunciado)
Como o enunciado pede o maior valor do resto -> r = (d-1), uma vez que o resto sendo igual ao divisor permite uma próxima divisão.
De 2 -> r + d + D = 178 -> (d-1) + d + D = 178 -> 2d + D = 179
De 1 -> 7d + (d-1) = D -> 8d - 1 = D
Juntando as equações azuis: 10d=180 -> d = 18
Consequentemente r = 17
Para encontrar D -> De 2 temos: 17+18+D=178 -> D = 143
Por fim: D + r = 143 + 17 = 160
Espero que entenda tudo.
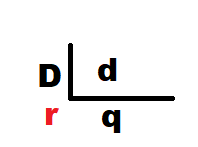
Daí,
1 - q.d + r = D ( da divisão como um todo)
2 - r + d + D = 178 (do enunciado)
Como o enunciado pede o maior valor do resto -> r = (d-1), uma vez que o resto sendo igual ao divisor permite uma próxima divisão.
De 2 -> r + d + D = 178 -> (d-1) + d + D = 178 -> 2d + D = 179
De 1 -> 7d + (d-1) = D -> 8d - 1 = D
Juntando as equações azuis: 10d=180 -> d = 18
Consequentemente r = 17
Para encontrar D -> De 2 temos: 17+18+D=178 -> D = 143
Por fim: D + r = 143 + 17 = 160
Espero que entenda tudo.
Paduan- Padawan
- Mensagens : 63
Data de inscrição : 03/03/2017
Idade : 26
Localização : São José dos Campos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
