Soluções reais de equações

por MillenaGuida Sex 17 Ago 2018, 10:54

Seja x solução real da equação √(x+9) + √(2x+17) = 12. Então a soma das soluções z, com Re z > 0, da equação
z⁴ = x - 32, é:

A)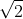 $Soluções reais de equações Gif$ (raiz de 2)
B)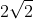 $Soluções reais de equações Gif$ (2 vezes raiz de 2)
C)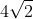 $Soluções reais de equações Gif$ (4 vezes raiz de 2)
D) 4
E) 16

Gostaria de saber como resolver essa questão que foi retirada de uma folha de revisão do curso para concursos militares.

por **Elcioschin** Sex 17 Ago 2018, 19:01

É fácil provar que x = 16

(z^4) = 16 - 32 ---> (z^2)^2 = - 16 ---> z^2 = 4.i ---> calcule z

por dekinho0 Sex 17 Ago 2018, 22:31

√(x+9) + √(2x+17) = 12

elevando ao quadrado têm-se

[√(x+9) + √(2x+17)]² = 12²

3x+26 +2√2x²+35x+153 =144

2√2x²+35x+153 =118-3x

eleva novamente ao quadrado

(2√2x²+35x+153)² =(118-3x)²
8x²+140x+612=13924-708x+9x²
x²-848x+13312=0

x=832
x'=16

logo,
z⁴ = x - 32
z⁴ = 16 - 32

z⁴ = -16

passando pra forma trigonométrica e utilizando a fórmula de Moivre
fica
z⁴ = 16(cos∏ + sen∏ i)

as raizes são
2(cos∏/4 + sen∏/4 i)= √2+√2i
2(cos3∏/4 + sen3∏/4 i)=- √2+√2i

2(cos5∏/4 + sen5∏/4 i)= -√2-√2i

2(cos7∏/4 + sen7∏/4 i)= √2-√2i
como z > 0 vc pega o 1º e 4º quadrante

√2+√2i somado a √2-√2i = 2√2

alternativa b.

Obs. como vc não postou o gabarito creio que seja essa.

Peço ao mestre Elcioschin que me corrija caso esteja errado.