Módulo e Equação do Segundo Grau

por Oziel Ter 26 Dez 2017, 16:29

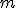Se $Módulo e Equação do Segundo Grau Mimetex_$ $Módulo e Equação do Segundo Grau Mimetex_$ , $Módulo e Equação do Segundo Grau Mimetex_$ e $Módulo e Equação do Segundo Grau Mimetex_$ , para todo $Módulo e Equação do Segundo Grau Mimetex_$ real, então os valores que o constante $Módulo e Equação do Segundo Grau Mimetex_$ pode assumir pertencem ao seguinte intervalo:

gabarito : [0,4]

por **Elcioschin** Ter 26 Dez 2017, 17:50

f(x) = |x| ---> g(x) = x² + m.x + m

f(g(x)) = g(x) ---> |x² + m.x + m| = x² + m.x + m

Para isto acontecer devemos m² + m.x + m ≥ 0

∆ = m² - 4.1.m ---> ∆ = m² - 4.m ---> Raízes m = 0 e m = 4

Como a função é uma parábola com a concavidade voltada para cima, se ela tiver 2 raízes reais, ela terá uma parte negativa. Para isto não acontecer devemos ∆ ≤ 0, assim, ela nunca será negativa.

Devemos ter, portanto, ∆ ≤ 0 ---> [0, 4]

por biologiaéchato Ter 26 Dez 2017, 17:52

Para que uma expressão sem módulo seja igual a seu módulo, ela deve ser positiva.
+x=|x|-->Sempre

Então, g(x) deverá assumir resultados maiores ou iguais á 0(Cruzar 1 vez o eixo x, ou nem cruzar).

Delta≤0
m²-4*1*m≤0
m²-4m≤0

Resolvendo, temos os zeros da função para x={0,4}.
A concavidade da parábola é para cima, então resultados negativos ficam para 0≤x≤4

Estudo do sinal:
++++++ 0 - - - - - - - - 4 +++++++

O intervalo que satisfaz a condição está entre 0 e 4.
Matematicamente:
S=[0,4] ou S={0≤x≤4}

Forte abraço e bons estudos!

por **Elcioschin** Ter 26 Dez 2017, 18:06

Duduu2525

Para ser sempre positiva, a parábola tem que estar acima do eixo x.
Isto significa que ela não pode cortar (∆ > 0) nem tangenciar (∆ = 0) o eixo x
Se ela cortar haverão duas raízes diferentes e se ela tangenciar haverá uma raiz dupla
Assim, para a função se sempre positiva as duas raízes deverão ser complexas. Neste caso só vale ∆ < 0

por biologiaéchato Ter 26 Dez 2017, 18:33

Boa tarde, Mestre Elcio.

Note que a equação m²-4m≤0 não diz nada á respeito da função g(x)=x²+mx+m, mas sim é o intervalo em que m satisfaz as condições do enunciado(a parábola ser sempre positiva ou nula).

Quanto ao sinal, tenho que discordar de você.
0 é considerado um resultado positivo(quando se estuda acerca de módulos), isto porquê, para resultados positivos temos |x|=x, e nesse caso, 0=|0|.

Provando experimentalmente:
m≤0(0 está contido na solução)
g(x)=x²+0m+0
g(x)=x²
f(g(x))=|x²|=x²

Está confirmado que f(g(x))=g(x)
Isto, porquê x^(Número Par)=Sempre positivo

Forte abraço!

por Oziel Seg 01 Jan 2018, 10:42

Não entendi esse final.

Se queremos delta maior ou igual a 0 porque não pegamos os valores menores que 0 ou maiores que 4 ? Por que tem que fazer delta menor que 0 ?

Eu sei que quando delta é menor que 0, m assume o mesmo sinal de a, mas não compreendo esse final. Pq o resultado fica desta maneira ?!

OBS: Minha primeira mensagem de 2018.

por **Elcioschin** Seg 01 Jan 2018, 11:03

Temos a função do 2º grau m² + m.x + m que deve ser maior ou igual a zero para que o módulo dela seja igual a ela.
Isto significa que a função NÃO pode ser negativa! Veja:

|5| = 5 ---> verdade
|0| = 0 ---> verdade
|-5| = - 5 ---> falso

Esta função tem como gráfico uma parábola com a concavidade voltada para cima. Para a função não ser negativa ele NÃO pode estar abaixo do eixo x, isto é, ela não pode ter duas raízes reais diferentes; ou ela tem uma raiz dupla ou tem duas raízes complexas conjugadas.

Logo, ou ∆ = 0 ou ∆ < 0 ---> Isto somente acontece no intervalo [0, 4]