Geometria plana - triangulo retangulo

As consequências no uso excessivo do computador não são imediatas, são doenças que vêm ao longo do tempo e que aumentam o risco se o usuário utilizar o computador por muitas horas seguidas e diariamente. É comum, um usuário, após o uso contínuo do computador, sentir cansaço, dores de cabeça, irritação nos olhos e fadiga. 
Dentre as medidas preventivas que podem ser tomadas para minimizar tais sintomas está o posicionamento correto do usuário frente ao monitor – a parte superior da tela deve estar diretamente à frente de seus olhos de modo que ao olhar para ela o usuário olhe levemente para baixo. 


Além disso, é recomendável que a distância da linha que passa pelo olhos do usuário até a tela tenha entre 50cm e 70cm. 

Na figura, o ponto O indica à posição do olho do usuário frente à tela de um monitor, T, um ponto do extremo superior e P, um ponto do extremo inferior da tela. Se um usuário se posicionar de tal modo que o ângulo TÔP tenha um acréscimo a, tal que 0 < a < pi/ 2 e cosa = 11√5/25 , então a distância de O a T, em relação à posição inicial, terá





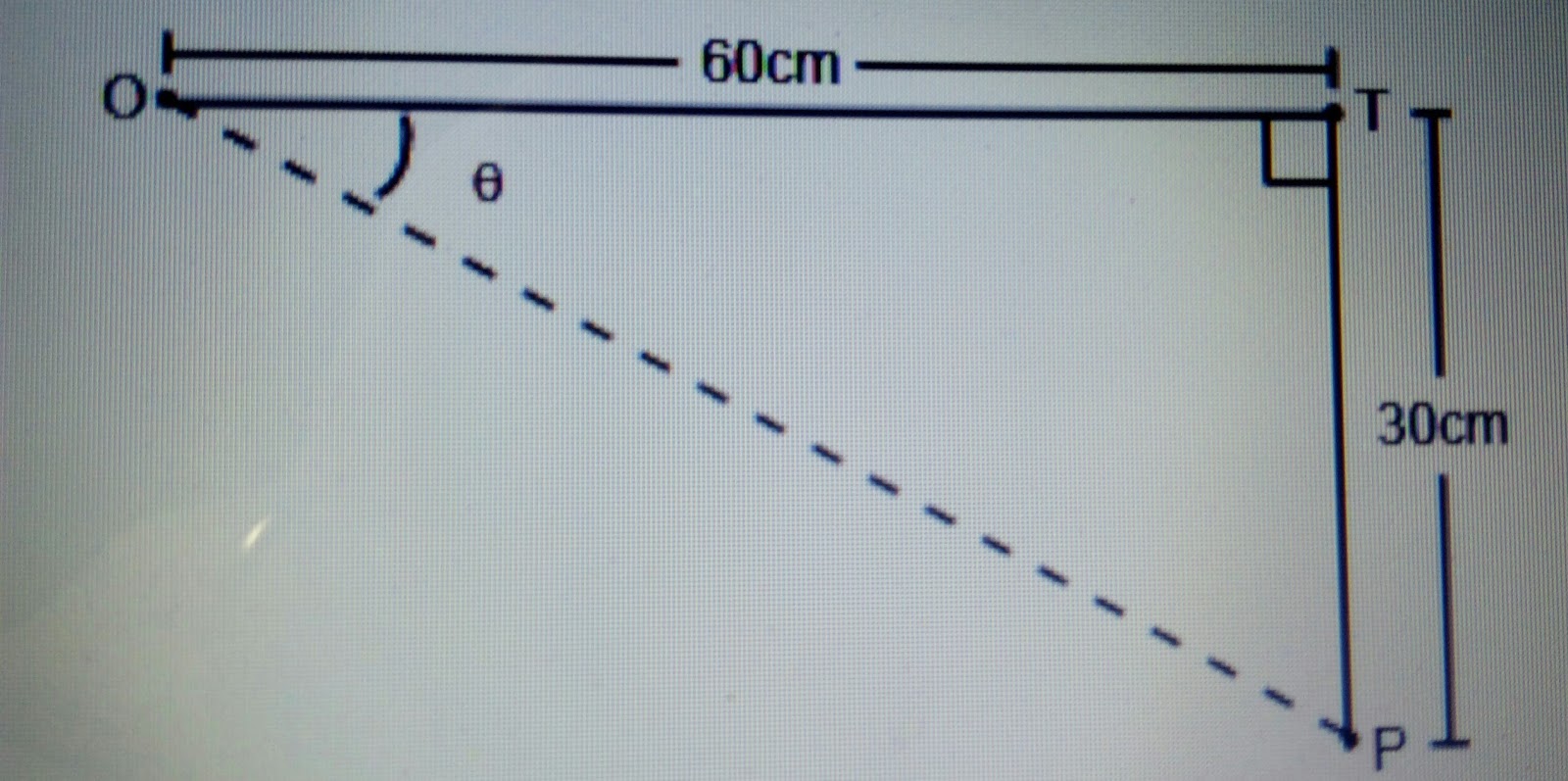
1) um acréscimo de 10cm.
2) um acréscimo de 15cm. 
3) um acréscimo de 20cm. 
4) um decréscimo de 15cm.
5) um decréscimo de 20cm. (resposta)

*Só consegui descobrir que o angulo teta vale 60°, depois nao consegui resolver

Vamos lá!

Você deve ter confundido as relações trigonométricas e feito o cosseno do ângulo teta para poder encontrar 60º. Na realidade, deveria ter utilizado a tangente pois nos foi dado o cateto oposto e o cateto adjacente. Feita essa observação, prossigamos.

tg θ = 30/60 ---> 1/2

Em θ acrescenta-se um ângulo a (0 < a < pi/2), então temos a nova situação (I):


Nos foi dado o cos a, logo, podemos encontrar a tg a
sen² a + cos² a = 1
sen² a + 11.5/625 = 1
sen² a = 20/625
sen a = 2√5/25

tg a = sen a/cos a ---> tg a = 2/11

Substituindo os dados em (I), temos:


Como o tamanho da tela não aumenta, temos a seguinte situação: Chamaremos de x o novo tamanho OT.


Logo o tamanho OT diminuiu 20 cm.