AFA 2005

Dada a função f definida por f(x)=x², considere a função real g definida por g(x)=f(x+m)+k, sendo m,k ε(pertencente) ℝ. É INCORRETO afirmar que:
(a) o gráfico da função g em relação ao gráfico da função f é deslocado k unidades para cima se k>0, e m unidades para a direita se m<0
(b)se m=0 e k=1, então o conjunto imagem de g é dado por Im={y ε ℝ | y≥1}
(c) se m= -2 e k= -3 , então as coordenadas do vértice da parábola que representa g são (-m,k)
(d)a equação do eixo de simetria da parábola que representa g é dada por x=m

gabarito= D
Bom ,eu só não entendi a letra b


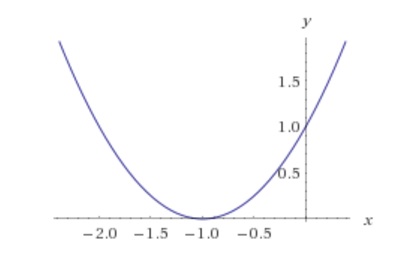
g(x) = x² + 2x + 1

o yv =0   então a imagem não deveria ser y >= 0?

a função f(x) = x² 

f(x+m) + k = para m=0 e k=1 --: f(X+0)+1 = f(x) + 1 = x² + 1

Xv = 0 e Yv = 0+1 = 1

portanto imagem = y ≥  1

Muito Obrigado!