Numeros Complexos ! Forma Trigonométrica...

Um terreno na forma de um paralelogramo tem o seu contorno desenhado, em um sistema de coordenadas cartesianas, de modo que os pontos O, A, B e C, nessa ordem, representam seus vértices consecutivos.
Sabendo-se que O é a origem do plano complexo, A é o afixo de e B é o afixo de , pode-se concluir que o ponto que representa o vértice C é o afixo de

a)

b)

c)

d)

e)


Pessoal não consegui visualizar a questão, para ver o q se pede !

Agradeço a quem resolver e se puder me explicar !

Obrigado

alissonsep,
Consegui visualizar a questão.Aviso de antemão que não tenho as habilidades estéticas do Euclides, mas vou fazer o possível
Primeiramente você deve calcular o modulo de A e B:
O de B basta multiplicar por raiz de 2, já que o ponto real e imaginario são iguais.Quanto A, que só tem valor real, deve ser escrito no eixo X :




Já que figura é um paralelogramo, vamos colocar o ponto C e suas componentes

Como você pode ver abaixo a componente Cy é igual a
Para saber Cx devemos fazer uma relação trigonometrica entre Cy e o modulo (cujo valor é o mesmo de BA).

Mas também ao olharmos a figura percebemos que os seguintes triangulos são iguais:
Vou resolver então o A-B-Bx.Chamando de X a distancia BA:
A-Bx =2 (Diferença no eixo X,para achar um dos catetos )



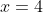
Temos agora:
Cx=
Cy=
OC=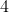
Arrumando o número C é igual a :

O angulo correspondente a ele é 300º,correspondente a , pois o seno é negativo e cosseno é positivo e tem os mesmos valores em módulo de 60º

O valor não bateu com nenhuma alternativa... vou rever pra ver se fiz algo errado.Não consegui ver nada incorreto.Se alguem tiver notado o deslize por favor poste aqui ^^

Caríssimo, vi seu erro!
estava sem consegui resolver essa questão também sua resolução me ajudou a resolvê-la! Muito Obrigado
O erro esta na hora de desenhar, veja que A e O são vertes consecutivos e não A e B, o gráfico esta errado os pontos reais de C acabam sendo -2 + 2iraiz3
o resto esta tudo certo, o afixo, termina sendo -1/2 + iraiz3/2, o que da o angulo de 120° letra D