Sequências

por Cristina Lins Sáb 01 Abr 2017, 13:58

Considere a sequência(an)n>=1 definida como indicada abaixo:
a1 = 1
a2 = 2 + 3
a3 = 4 + 5 + 6
a4 = 7 + 8 + 9 +10

a) O termo a10 é a soma de 10 inteiros consecutivos. Qual é o menor e o maior desses inteiros?

b) Calcule a10.

c) Forneça uma expressão geral para o termo an.

por **ivomilton** Sáb 01 Abr 2017, 15:37

Cristina Lins escreveu:Considere a sequência(an)n>=1 definida como indicada abaixo:
a1 = 1
a2 = 2 + 3
a3 = 4 + 5 + 6
a4 = 7 + 8 + 9 +10

a) O termo a10 é a soma de 10 inteiros consecutivos. Qual é o menor e o maior desses inteiros?

b) Calcule a10.

c) Forneça uma expressão geral para o termo an.

Boa tarde, Cristina.

an = n(n+1)/2

a,b)
a10 = 10(10+1)/2 = 10*11/2 = 110/2 = 55 (o maior da 10ª linha)

O menor deverá ser:
55 - 10 + 1 = 46

c) an = n(n+1)/2

Um abraço.

por **petras** Sáb 01 Abr 2017, 15:40

a) O primeiro inteiro da soma que define a10:
\frac{1}{2}(n-1)n+1
\\ \frac{1}{2}(1-1)1+1=1\\\ \frac{1}{2}(2-1)2+1=2\\\ \frac{1}{2}(3-1)3+1=4...\\\ \frac{1}{2}(10-1)10+1=46

O último inteiro da soma que define an:
a1 = 46 Portanto para a10 o último termo será 46+10-1==55

b) a10 = Soma PA.

a10 = (46+55).10/2 = 505

c) an = Soma PA com n termos:
a1=\frac{1}{2}(n-1)n+1

an=\frac{1}{2}(n-1)n+1+(n-1)=\frac{1}{2}(n-1)n+n

an=[\frac{1}{2}(n-1)n+1]+[\frac{1}{2}(n-1)n+n] \cdot \frac{n}{2}

an=[\frac{n^2-n+2+n^2-n+2n}{2}]\cdot \frac{n}{2}=\frac{2(n^2+1)}{2}\cdot \frac{n}{2}=\frac{n^3+n}{2}

por **petras** Sáb 01 Abr 2017, 15:43

Mestre Ivomilton, creio que equivocou-se. a10 não é o décimo termo de a10.
a10 corresponde ao somatório dos 10 termos de a10.

por Cristina Lins Sáb 01 Abr 2017, 17:44

Petras, boa tarde

Antes de mais nada, obrigada pela ajuda.
Só não entendi, como que chego na fórmula
{[(n - 1) n] : 2} + 1.

Você poderia me ajudar?

por Cristina Lins Sáb 01 Abr 2017, 17:47

obrigada Ivomilton pela atenção

Um abraço

por **petras** Sáb 01 Abr 2017, 18:27

Não existe uma regra para determinar a lei de formação de uma sequência. Vai mais da prática e da capacidade de visualização e da experimentação de cada um.

por Cristina Lins Sáb 01 Abr 2017, 18:53

Obrigada. Valeu!!!! Entendi o restante do exercício

por Mathematicien Sáb 01 Abr 2017, 19:20

petras escreveu:Não existe uma regra para determinar a lei de formação de uma sequência. Vai mais da prática e da capacidade de visualização e da experimentação de cada um.

Mas como você chegou a essa lei de formação?

por **fantecele** Ter 30 maio 2017, 19:26

Uma maneira de encontrar uma fórmula para o primeiro termo de cada 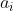$a_{i}$ (i = 1, 2, 3, 4, ...) é:

Vamos definir a sequência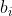 $b_{i}$ (i = 1, 2, 3, 4, ...) formada pelos primeiros termos de cada 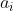$a_{i}$ , ou seja $b_{1}=1;b_{2}=2;b_{3}=4;b_{4}=7;...$ .

Podemos perceber que:
$\\b_{2}-b_{1}=1\\b_{3}-b_{2}=2\\b_{4}-b_{3}=3\\b_{5}-b_{4}=4\\...\\b_{n}-b_{n-1}=n-1$

Somando tudo:
$\\b_{n}-b_{1}=\frac{(n-1).n}{2}\\b_{n}=\frac{(n-1).n}{2}+1$

Com isso encontrarmos a fórmula para os primeiros termos, agora para encontrar o " $\\a_{n}$ " basta fazer igual como o petras fez.