Duvida - Vetores

por BallaHalls Sáb 11 Mar 2017, 01:33

Como não encontrei um forum de vetores, decidi postar no qual mais se assemelha, Algebra. Me desculpem se existir um local mais adequado.

Em um triangulo ABC qualquer, AD é a bissetriz do angulo A. Exprimir D-A em função de B-A e C-A.
Assim como na figura abaixo
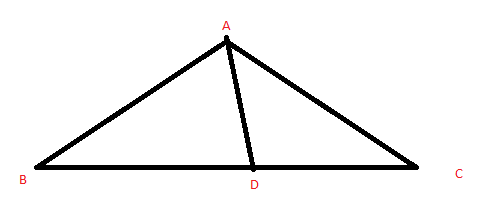
Duvida - Vetores 2wda4b9

Gabarito

Spoiler:

por **Forken** Sáb 11 Mar 2017, 03:15

\\\overrightarrow{AB}=(x,y)\\ \overrightarrow{AC}=(z,w)\\\\\widehat{A}=\Theta;\;B\widehat{A}D=C\widehat{A}D=\frac{\Theta}{2},\;\forall \;\Theta\;tal\;que\;\widehat{A}+\widehat{B}+\widehat{C}=180^{\circ}\\\\B-A+C-A=D-A\Leftrightarrow \overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\Leftrightarrow (x,y)+(z,w)=(x+z,y+w)=\;=\overrightarrow{AD}

Foi a única coisa que consegui pensar, seria interessante você estipular valores e verificar se está correto, pois não tenho certeza. Observei e criei a hipótese, agora você experimenta Very Happy

por BallaHalls Sáb 11 Mar 2017, 15:33

Desculpa, não consegui entender como você fez a soma desses vetores. :/

por **Forken** Sáb 11 Mar 2017, 15:49

Quando junta as origens de 2 vetores, o vetor resultante que no caso é o vetor AD, "sai" da origem. Não tenho certeza se a resolução está correta, sugiro que você pegue diferentes triângulo com suas respectivas medidas e teste.

por BallaHalls Sáb 11 Mar 2017, 16:59

Mas ai seria uma subtração de vetores. Mas não sei se seria valido no triangulo, ja que a definição da subtração de vetores é em um quadrilatero.
Tentei mudar os vetores de posição e re-arranjalos, mas n achei nada que exprima \overrightarrow{AD} Na verdade mechendo com os angulos, achei que \overrightarrow{AB}=\overrightarrow{AC} mas não sei se estou certo :/

por BallaHalls Dom 12 Mar 2017, 12:43

Desculpa o spam, é que eu achei uma resposta. Segue abaixo:

Pela definição de subtração de vetores, tiramos que:
\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB} (I)

E observa-se que
\overrightarrow{BC}=\overrightarrow{BD}+\overrightarrow{DC} (II)

Usando o teorema d bissetriz interna, nós temos
\frac{\overrightarrow{AB}}{\overrightarrow{BD}}=\frac{\overrightarrow{AC}}{\overrightarrow{DC}} (III)

Observando o triangulo ADC, tiramos
\overrightarrow{DC}=\overrightarrow{AC}-\overrightarrow{AD} (IV)

De II, tiramos:
\overrightarrow{BD}=\overrightarrow{BC}-\overrightarrow{DC}
Substituindo em I e III encontra-se
\frac{\overrightarrow{AB}}{\overrightarrow{AC}}=\frac{\overrightarrow{AC}-\overrightarrow{AB}}{\overrightarrow{DC}}-1

Substituindo IV, encontra-se:
\frac{\overrightarrow{AB}}{\overrightarrow{AC}}=\frac{\overrightarrow{AC}-\overrightarrow{AB}}{\overrightarrow{AC}-\overrightarrow{AD}}-1

Isolando \overrightarrow{AD}

\overrightarrow{AD}=\frac{\overrightarrow{AB}}{\overrightarrow{AC}}+\overrightarrow{AB}

por **Medeiros** Dom 12 Mar 2017, 17:25

Tenho minhas dúvidas sobre essa resposta. De início, o teorema da bissetriz interna é aplicado sobre os módulos dos vetores citados; e os vetores em si, além do módulo, têm direção e sentido.

Para efeitos de confirmação da resposta, tomamos o exemplo simples de um triângulo isósceles conforme desenhado. Aquela resposta deve valer também para este exemplo, no qual já sabemos que o vetor AD = (0, -4). O fato é que não vejo como obter este valor de AD a partir da solução apresentada.