ESPM-SP Geometria e Semelhança de Triângulos

Na figura abaixo, A'C' é paralelo a AC e B'C' é paralelo a BC.
Se a área do triângulo ABC é igual a 4m², a área do triângulo A'B'C' é:


Gabarito: 25m²


OBS: Cheguei até a razão entre A'B'/AB, mas não consegui achar a área pedida.

Olá amigo, boa noite.

Determinado que ∆ABC ~ ∆A'B'C' chegamos na relação:

A'B'/AB = K (onde K é a razão de semelhaça)

Conhecemos o ponto A (1;3) e B(2;1), portanto podemos calcular o comprimento de AB:

AB² = (∆x)²+(∆y)² → AB² = 1²+2² → AB = √5

Conhecendo 2 pontos de uma reta, podemos determinar sua equação:

Sendo a reta da forma y=mx+t, m = ∆y/∆x = -2/1 = -2. ∴ m = -2.
y = -2x+t, A(1;3), substituindo: 3 = -2 +t ∴ t = 5

Logo a equação da reta é dada por y = -2x+5 

Pela figura sabemos que A', A, B, B' são colineares, portanto a reta passa por A' e B'. 

Para A', x = 0 ∴ y = 5. A'(0;5)
Para B', y = 0 ∴ x = 5/2. B'(5/2;0)

Podemos então calcular o comprimento A'B':

(A'B')² = (5/2)²+5² → (A'B') = 25/4 + 100/4 ∴ A'B' = 5√5/2

Voltando agora na relação A'B'/AB = K e substituindo os valores encontrados:



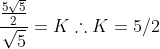
Sabemos que a relação entre as áreas de dois triângulos semelhantes é dada por : (onde ''[]'' representa área)
[A'B'C']/[ABC]= K² → [A'B'C']= K².[ABC]　→ [A'B'C'] = (25/4).4 →
→ [A'B'C'] = 25m²